ΑΛΓΕΒΡΑ Α΄ ΛΥΚΕΙΟΥ
 Για το πως μπορούμε να απαλλαγούμε από τις απόλυτες τιμές που τυχόν εμφανίζονται σε μία αλγεβρική παράσταση έχουμε αναφερθεί σε προηγούμενο άρθρο μας (και καλό θα ήταν να του ρίξετε μια ματιά κάνοντας κλικ εδώ). Σε αυτή τη δημοσίευση θα ασχοληθούμε με εξισώσεις στις οποίες ο άγνωστος βρίσκεται πίσω από τις μπάρες της απόλυτης τιμής. Εξισώσεις δηλαδή που ο άγνωστος είναι «φυλακισμένος» μέσα σε μία ή και περισσότερες απόλυτες τιμές. Σκοπός μας σε μια τέτοια εξίσωση (όπως και σε κάθε εξίσωση άλλωστε) είναι να βρούμε ποιος αριθμός είναι «κρυμμένος πίσω από τη μάσκα του x». Στόχος μας είναι να «ελευθερώσουμε» το x μέσα από την απόλυτη τιμή. Για να το καταφέρουμε αυτό ας θυμηθούμε πρώτα τι είναι η απόλυτη τιμή ενός αριθμού και μετά βλέπουμε πως λύνουμε την εξίσωση.
Για το πως μπορούμε να απαλλαγούμε από τις απόλυτες τιμές που τυχόν εμφανίζονται σε μία αλγεβρική παράσταση έχουμε αναφερθεί σε προηγούμενο άρθρο μας (και καλό θα ήταν να του ρίξετε μια ματιά κάνοντας κλικ εδώ). Σε αυτή τη δημοσίευση θα ασχοληθούμε με εξισώσεις στις οποίες ο άγνωστος βρίσκεται πίσω από τις μπάρες της απόλυτης τιμής. Εξισώσεις δηλαδή που ο άγνωστος είναι «φυλακισμένος» μέσα σε μία ή και περισσότερες απόλυτες τιμές. Σκοπός μας σε μια τέτοια εξίσωση (όπως και σε κάθε εξίσωση άλλωστε) είναι να βρούμε ποιος αριθμός είναι «κρυμμένος πίσω από τη μάσκα του x». Στόχος μας είναι να «ελευθερώσουμε» το x μέσα από την απόλυτη τιμή. Για να το καταφέρουμε αυτό ας θυμηθούμε πρώτα τι είναι η απόλυτη τιμή ενός αριθμού και μετά βλέπουμε πως λύνουμε την εξίσωση.
Η απόλυτη τιμή ενός αριθμού ορίζεται και αλγεβρικά και γεωμετρικά. Εμείς θα αρκεστούμε στο δεύτερο μιας και είναι αρκετό για να στηριχτούμε σε αυτό και να καταφέρουμε να λύσουμε τις εξισώσεις.
Τι είναι λοιπόν η απόλυτη τιμή;
Γνωρίζουμε ότι κάθε πραγματικός αριθμός x παριστάνεται με ένα σημείο πάνω στον άξονα των πραγματικών αριθμών. Την απόσταση του σημείου αυτού από το 0 τη λέμε απόλυτη τιμή του αριθμού x και τη συμβολίζουμε |x|.

Έτσι μπορούμε να εξηγήσουμε και πολλές από τις ιδιότητες της απόλυτης τιμής όπως
Η απόλυτη τιμή οποιουδήποτε αριθμού είναι είτε θετικός αριθμός είτε μηδέν, γιατί όπως είναι γνωστό αρνητική απόσταση δεν υπάρχει. Έτσι έχουμε,
Οι αντίθετοι αριθμοί έχουν την ίδια απόλυτη τιμή, αφού ισαπέχουν από το 0.
Ας δούμε τώρα τι γίνεται με τις εξισώσεις.
Σας θυμίζω ότι για να αντιλαμβανόμαστε καλύτερα τις εξισώσεις μπορούμε να τις θεωρούμε σαν ερωτήσεις. Έτσι η εξίσωση |x|= -5 , μας ρωτάει ποιος αριθμός είναι αυτός που απέχει από το 0 -5 μονάδες; Προφανώς η απάντηση είναι κανένας (αναφέραμε και πιο πάνω ότι δεν νοείται αρνητική απόσταση). Ενώ η απάντηση στην ερώτηση(=εξίσωση) |x|=0 είναι «ο μοναδικός αριθμός που απέχει από το μηδέν 0 μονάδες είναι ο 0». Όμως η εξίσωση |χ|=2 μας ζητάει να βρούμε τον αριθμό που απέχει από το 0 2 μονάδες. Η απάντηση είναι ότι δεν υπάρχει μόνο ένας αριθμός με αυτή την ιδιότητα αλλά δύο αριθμοί ο 2 και ο -2. Έτσι η εξίσωσή μας έχει δύο λύσεις τις x=2 ή x= -2. Για να γενικεύσουμε λίγο τα πράγματα και να τα βάλουμε σε μία τάξη δείτε το παρακάτω σχεδιάγραμμα.

Όπου βλέπετε f(x) θα εννοούμε «μια παράσταση που περιέχει x». Γιατί μέσα στο απόλυτο δεν είναι απαραίτητο να υπάρχει μόνο x, μπορεί κάποιοι «κακοί μαθηματικοί» (σαν κι εμένα) να ζητήσουν να λυθούν εξισώσεις που μέσα στο απόλυτο να υπάρχουν αρκετά πράγματα.
Για να λύσουμε οποιαδήποτε εξίσωση στην οποία το x βρίσκεται μέσα σε απόλυτο, πρέπει να στηριχτούμε στα συμπεράσματα του παραπάνω πίνακα. Πρέπει λοιπόν να απομονώσουμε το απόλυτο στο ένα μέλος και μετά κοιτώντας τι ρόλο παίζει το άλλο μέλος να αποφανθούμε αν η εξίσωση έχει λύσεις ή όχι και στην περίπτωση που έχει ποιες είναι αυτές. Ας δούμε τώρα μερικά παραδείγματα:
Άσκηση 1: Να λυθεί η εξίσωση 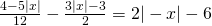
[gn_spoiler title=»Λύση:»]Φαίνεται η εξίσωση μας να έχει δύο διαφορετικές απόλυτες τιμές την |x| και την |-x|. Αυτό όμως δεν αληθεύει γιατί ξέρουμε ότι |-x|=|x|. Οπότε μπορούμε στην εξίσωση που μας δώσανε όπου έχει |-x| εμείς να βάλουμε |x|. Για να απομονώσουμε το απόλυτο που θέλουμε θα ακολουθήσουμε τη γνωστή διαδικασία που ακολουθούμε σε όλες τις εξισώσεις α΄ βαθμού.
Πρώτα θα διώξουμε τους παρονομαστές πολλαπλασιάζοντας κάθε όρο με το Ε.Κ.Π. των παρονομαστών που είναι το 12
![]()
![]()
Τώρα διώχνουμε τις παρενθέσεις κάνοντας χρήση της επιμεριστικής ιδιότητας
![]()
Χωρίζουμε τους γνωστούς από τους άγνωστους ώστε να μπορέσουμε να συνεχίσουμε τις πράξεις χωρίς να ξεχνάμε ότι προς το παρόν άγνωστος είναι το |x| κι όχι το x
![]()
![]()
άρα
![]()
ή πιο απλά
![]()
Αφού καταφέραμε κι απομονώσαμε το απόλυτο μπορούμε σύμφωνα με όσα έχουμε πει πιο πάνω ν΄απαντήσουμε ότι ![]() ή
ή ![]()
[/gn_spoiler]
Άσκηση 2: Να λυθεί η εξίσωση 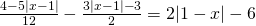
[gn_spoiler title=»Λύση:»]Όπως θα παρατηρήσατε η εξίσωση αυτή είναι ίδια με την προηγούμενη με την μόνη αλλαγή αντί για |x| έχουμε |x-1|. Και πάλι επειδή οι αριθμοί 1-x και x-1 είναι αντίθετοι η εξίσωση θα γίνει
![]()
και θα λυθεί με τον ίδιο ακριβώς τρόπο καταλήγοντας στο
![Rendered by QuickLaTeX.com \[|x-1|=2 \Leftrightarrow\left\{\begin{matrix}x-1=-2\Leftrightarrow x=-2+1=-1\\ \eta\\x-1=2\Leftrightarrow x=2+1=3\end{matrix}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-3d8b31a9400dddc58f39cee2363a52b1_l3.png)
Έτσι λοιπόν βλέπουμε ότι αν τα απόλυτα που έχουμε στην εξίσωση περιέχουν ίσες ή ακόμη και αντίθετες παραστάσεις, τότε δεν μας ενδιαφέρει το περιεχόμενη της απόλυτης τιμής. Λύνουμε την εξίσωση κανονικά όπως όλες τις εξισώσεις «κουβαλώντας» το απόλυτο μέχρι να καταφέρουμε να το απομονώσουμε και στο τέλος το πετάμε (πάντα σύμφωνα με το διάγραμμα που έχουμε παραπάνω).
Επειδή κάποιοι μπορεί να «ψιλό» μπερδεύονται κουβαλώντας το απόλυτο μπορούν να γλυτώσουν από αυτό με την συνηθισμένη στα μαθηματικά μέθοδο: «αν κάτι μ΄ενοχλεί κάνω πως δεν το βλέπω». Έτσι λοιπόν θα μπορούσαμε να θέσουμε όπου |x-1|=α (σχέση 1) και να λύσουμε την εξίσωση χωρίς το απόλυτο. Μόλις ξεμπερδέψουμε με το α και το βρούμε γυρίζουμε και το αντικαθιστούμε στη σχέση 1 απ’ όπου υπολογίζουμε το x που μας ενδιαφέρει.
Watch me 
Θέτω |χ-1|=α (σχέση 1) οπότε η εξίσωση γίνεται
![]()
![]()
![]()
![]()
![]()
Ας μην ξεχνάμε όμως ότι δεν ψάχναμε το α αλλά το x. Πάμε λοιπόν στη σχέση 1 και αντικαθιστούμε όπου α=2, οπότε
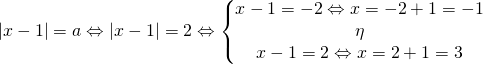
Τη μέθοδο αυτή για να είμαι ειλικρινής δεν σας την έδειξα μόνο για την περίπτωση που κάποιος δυσκολεύεται με τα πολλά απόλυτα αλλά και γιατί σε κάποιες περιπτώσεις θα έλεγα δεν μπορούμε να την αποφύγουμε γι’ αυτό καλό είναι να την ξέρουμε. Δείτε την επόμενη άσκηση και θα καταλάβετε. [/gn_spoiler]
Άσκηση 3: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση 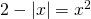
[gn_spoiler title=»Λύση:»] Την άσκηση αυτή θα μπορούσαμε να τη λύσουμε απομονώνοντας το απόλυτο στο ένα μέλος, οπότε η εξίσωση να γίνει |x|=2 – x2 αλλά πιστεύω ότι έτσι δεν θα μας συνέφερε γιατί το δεύτερο μέλος (το 2 – x2) δεν γνωρίζουμε αν είναι θετικός ή αρνητικός αριθμός ( για κάποιες τιμές του x γίνεται θετικός, για κάποιες αρνητικός και για κάποιες γίνεται ίσος με 0). Έτσι θα έπρεπε να διακρίνουμε περιπτώσεις και να πούμε
Περίπτωση 1η: αν το 2 – x2 είναι αρνητικό η εξίσωσή μας είναι αδύνατη (βλέπε και το σχεδιάγραμμα πιο πάνω)
Περίπτωση 2η: αν ![]() , τότε x=2-x2 ή x= – (2-x2 ) και να λύσω δύο εξισώσεις (δεύτερου βαθμού η καθεμία) κι αφού βρω τις λύσεις να κρατήσω από αυτές μόνο εκείνες που επαληθεύουν τον περιορισμό
, τότε x=2-x2 ή x= – (2-x2 ) και να λύσω δύο εξισώσεις (δεύτερου βαθμού η καθεμία) κι αφού βρω τις λύσεις να κρατήσω από αυτές μόνο εκείνες που επαληθεύουν τον περιορισμό ![]() .
.
Για να γλυτώσουμε όλη αυτή τη δουλειά μπορούμε να σκεφτούμε λίγο πιο έξυπνα και να αντικαταστήσουμε το |x| με έναν άλλο αριθμό έστω α. Τότε θα έχουμε γλυτώσει και από το |x| αλλά και από το x2 γιατί το x2=|x2|=|x|2=α2 (ρίξε μια ματιά στις ιδιότητες των απολύτων). Ας δούμε τώρα πως έχει καταντήσει η εξίσωσή μας θέτοντας |x|=α,
![]()
Η διακρίνουσα του τριωνύμου είναι
![]()
και οι λύσεις της εξίσωσης αυτής είναι
![]()
ή
![]()
Εύκολα λοιπόν βρήκαμε το α, το x όμως είναι αυτό που μας ενδιαφέρει
![Rendered by QuickLaTeX.com \[\left | x \right |=\alpha \Leftrightarrow \left\{\begin{matrix} \left | x \right |=1 \Leftrightarrow x=\pm 1\\\eta'\\ \left | x \right |=-2 & \alpha \delta \upsilon \nu \alpha \tau \eta \end{matrix}\right.\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-198fbd64d110d48053f6e400aa566f03_l3.png)
[/gn_spoiler]
Άσκηση 4: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση 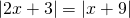
[gn_spoiler title=»Λύση:»] Στην άσκηση αυτή ανήκει στη γενική κατηγορία
![]()
και λύνεται με την ισοδυναμία
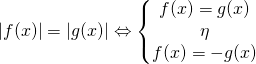
Έχουμε λοιπόν 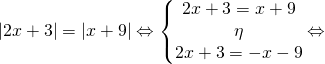
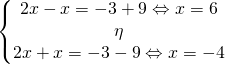 [/gn_spoiler]
[/gn_spoiler]

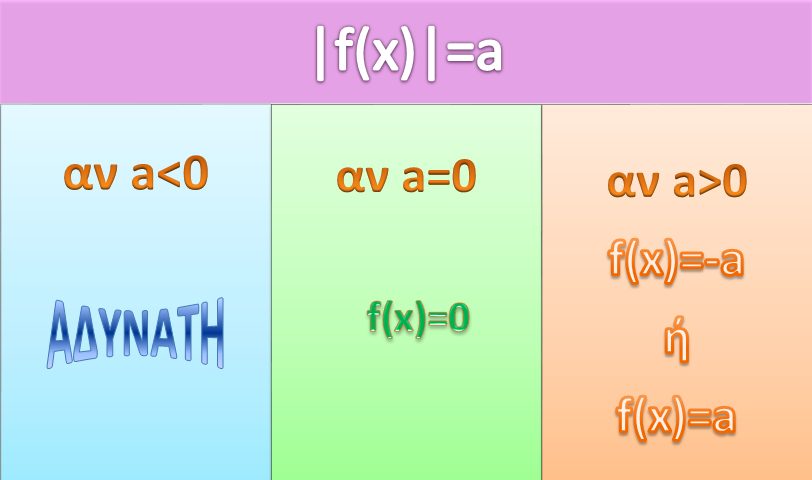
Πολύ καλό!!
Ευχαριστώ πάρα πολύ!!
τι πεδίο ορισμού βάζουμε σε μία συνάρτηση f(x)= |x-1| ??
Αφού δεν υπάρχει κανένας περιορισμός (από παρονομαστή, ριζικό, λογάριθμο, εφαπτομένη ή συνεφαπτομένη ) το πεδίο ορισμού είναι το σύνολο των πραγματικών αριθμών. Αν θες ρίξε μια ματιά εδώ κι εδώ
Η λύση
είναι σωστή; Χρειάζεται να γράψουμε κάτι περισσότερο;
Είναι σωστή και δεν χρειάζεται τίποτε άλλο.
ΕΙΜΑΙ Η ΣΤΑΜΑΤΙΑ . ΠΑΩ ΠΡΩΤΗ ΛΥΚΕΙΟΥ. ΤΟ SITE ΣΑΣ ΕΙΝΑΙ ΠΟΛΥ ΕΝΔΙΑΦΕΡΟΝ . ΘΑ ΗΘΕΛΑ ΝΑ ΜΕ ΔΕΧΘΗΤΕ . ΣΤΟΧΟΣ ΜΟΥ ΝΑ ΒΓΑΖΩ ΑΠΟ ΤΑ ΚΑΓΚΕΛΑ ΤΑ ΑΠΟΛΥΤΑ , ΝΑ ΞΕΡΙΖΩΝΩ ΤΙΣ ΡΙΖΕΣ , ΝΑ ΔΙΑΚΡΙΝΩ ΤΙΣ ΔΙΑΚΡΙΝΟΥΣΕΣ, ΚΑΙ ΝΑ ΜΑΘΩ ΤΙΣ ΠΙΘΑΝΟΤΗΤΕΣ ΓΙΑ ΝΑ ΓΡΑΨΩ ΚΑΛΑ ΣΤΟ ΤΕΛΟΣ. ΜΟΥ ΑΡΕΣΕΙ ΠΟΛΥ Η ΠΟΙΗΣΗ ΑΛΛΑ ΚΥΡΙΩΣ Η ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ.
για πιο λογο στην ασκηση 2 ειπατε στην δευτερη σειρα εξισωσης οτι απολυτο χ-1 ισο με 2
Δημήτρη, αν παρατηρήσεις καλά την εξίσωση της 1ης άσκησης και την εξίσωση της 2ης άσκησης θα δεις ότι μοιάζουν πάρα μα πάρα πολύ. Στην πραγματικότητα είναι η ίδια εξίσωση το μοναδικό πράγμα που αλλάζει είναι το απόλυτο. Στην πρώτη εξίσωση υπάρχει το |χ| ενώ στη δεύτερη τη θέση του έχει πάρει το |χ-1|. Αφού λοιπόν στην άσκηση 1 λύσαμε την εξίσωση με άγνωστο το |χ| και καταλήξαμε στο ότι |χ|=2 θεώρησα καλό να μην την ξαναλύσω στην δεύτερη άσκηση αφού η διαδικασία της λύσης θα ήταν ακριβώς η ίδια. Πήγα λοιπόν κατευθείαν στο τελικό βήμα που είναι το |χ-1|=2. Στην συνέχεια βάζουμε το απόλυτο και παίρνουμε τις δύο περιπτώσεις που αναφέρουμε στο άρθρο, δηλαδή |χ-1|=2 ή |χ-1|=-2.
Δηλαδη ,παραλειψαμε αυτο που ενοούταν ή αν θελετε αυτο π λυθηκε στην προηγουμενη
ασκηση και απλα συνεχισαμε λυνωντας την ακηση???
Ακριβώς έτσι, όπως τα λες.
Ευχαριστω πολύ φιλε μ ,με βοηθησες παρα πολυ ….αν χρειαστώ κατι περαιτέρω θα σε ειδοποιήσω.
Πως γραφεται η f χωρις απολυτο F(χ)=|χ-1|
Από τις ιδιότητες των απολύτων τιμών γνωρίζουμε ότι ισχύουν τα παρακάτω: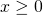 τότε
τότε 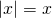 ενώ
ενώ έχουμε
έχουμε 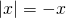 . Έτσι λοιπόν για να δίωξεις το απόλυτο πρέπει να γνωρίζεις πότε το «περιεχόμενό» του, το x-1 δηλαδή, είναι θετικό και πότε αρνητικό. Λύνεις λοιπόν την ανίσωση:
. Έτσι λοιπόν για να δίωξεις το απόλυτο πρέπει να γνωρίζεις πότε το «περιεχόμενό» του, το x-1 δηλαδή, είναι θετικό και πότε αρνητικό. Λύνεις λοιπόν την ανίσωση:
αν
όταν
ξέρεις τώρα ότι η παράσταση x-1 είναι αρνητική όταν το x είναι μικρότερο του 1 και προφανώς είναι μεγαλύτερη ή ίση με το 0 όταν το x είναι μεγαλύτερο ή ίσο του 1. Από τα παραπάνω βγάζεις το συμπέρασμα ότι:
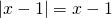 όταν
όταν 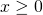
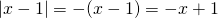 όταν
όταν 
και
Επομένως για τη συνάρτηση θα έχεις:
Όταν λείπει το γ από μια εξίσωση.. τι κάνουμε…?
Εύη, υποθέτω ότι αναφέρεσαι σε εξίσωση δεύτερου βαθμού, δηλαδή σε εξίσωση της μορφής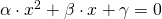 με
με 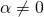 . αλλά και το γ=0. Επομένως θα έχεις μια εξίσωση έτσι:
. αλλά και το γ=0. Επομένως θα έχεις μια εξίσωση έτσι: 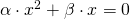 . Μια τέτοια εξίσωση λύνεται κανονικά όπως όλες οι εξισώσεις δεύτερου βαθμού και τον τρόπο θα τον βρεις εδώ.
. Μια τέτοια εξίσωση λύνεται κανονικά όπως όλες οι εξισώσεις δεύτερου βαθμού και τον τρόπο θα τον βρεις εδώ.
Όμως αν όπως λες το γ=0, τότε μπορεί να λυθεί και διαφορετικά: Να βγάλουμε κοινό παράγοντα το x και στη συνέχεια να πούμε ότι κάθε παράγοντας του γινομμένου που προέκυψε πρέπει να είναι ίσος με το μηδέν. Να μετατρέψουμε δηλαδή τη δευτεροβάθμια εξίσωση σε γινόμενο δύο πρωτοβάθμιων. Κοιτα το παρακάτω παράδειγμα για να καταλάβεις τι εννοώ:
|χ-1|=2
χ-1=2 ή χ-1=-2
χ=3 ή χ=-1
είναι σωστο ;
Ναι είναι σωστό.
pws tha luthei an exei apoluto mesa sto apoluto? p.x |2|x|-7|=5
Πρώτα διακρίνεις περιπτώσεις για την παράσταση που βρίσκεται μέσα στο «μεγάλο» απόλυτο:
ΠΕΡΙΠΤΩΣΗ 1η: Αν
τότε
ισοδύναμα
Αν
τότε
και οι δύο λύσεις δεκτές αφού ικανοποιούν τον περιορισμό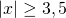
ΠΕΡΙΠΤΩΣΗ 2η: Αν
τότε
ισοδύναμα
Αν
τότε
και οι δύο λύσεις δεκτές αφού ικανοποιούν τον περιορισμό
kai an einai aniswsh pws ginetai? p.x. -3<_|-2x+1|<_0
Τάσο, για το θέμα αυτό είχα σκοπό να γράψω ένα άρθρο για να προσπαθήσω να ξεδιαλύνω τα δύσκολα σημεία. Επειδή όμως υποψιάζομαι ότι τη βιάζεσαι την απάντηση θα προσπαθήσω μέσα από την άσκηση να δώσω τον τρόπο αντιμετώπισης τέτοιου είδους ασκήσεων.
Για να λύσουμε λοιπόν μια ανίσωση που ο άγνωστος είναι φυλακισμένος μέσα σε απόλυτες τιμές πρέπει όπως και στις εξισώσεις να ελευθερώσουμε τον άγνωστο και στη συνέχεια να λύσουμε την ανίσωση κανονικά. Αυτό όμως πρέπει να γίνει στηριζόμενοι στις ιδιότητες των απολύτων τιμών. Οι ιδιότητες που μας χρειάζονται εδώ είναι δύο:
Πρώτη:
όπου το θ είναι αριθμός μεγαλύτερος του μηδενός, γιατί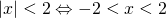
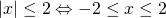
αν το θ είναι μικρότερο από το μηδέν η ανίσωση είναι αδύνατη (σου θυμίζω ότι η απόλυτη τιμή είναι πάντα αριθμός μη αρνητικός). Πάρε για παράδειγμα την ανίσωση |χ|< -5. Η ανίσωση αυτή δεν έχει λύση αφού κανενός αριθμού η απόλυτη τιμή δεν είναι μικρότερη του 0 πόσο μάλλον μικρότερη του -5. αν το θ είναι ίσο με το μηδέν τότε η ανίσωση έχει μοναδική λύση την χ=0. Δηλαδή η |χ|=0 μας δίνει χ=0 και αυτό γιατί ο μοναδικός αριθμός που έχει απόλυτη τιμή ίση με μηδέν είναι το μηδέν. Ας συγκεντρώσουμε τώρα τα παραπάνω να καταλάβουμε τι γίνεται.
Η ανίσωση |χ|=0 έχει λύση χ=0
Η ανίσωση |χ|<0 είναι αδύνατη
Η ανίσωση |χ|< -2 δεν έχει λύση Η ανίσωση
Η ανίσωση
Δεύτερη:
Κι εδώ θεωρούμαι ότι το θ είναι θετικός αριθμός όπως και προηγούμενα.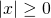 έχει λύση όλους τους αριθμούς ακόμη και το μηδέν
έχει λύση όλους τους αριθμούς ακόμη και το μηδέν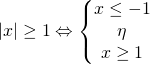
αν το θ είναι αρνητικός αριθμός τότε η ανίσωση είναι αόριστη γιατί για παράδειγμα:
Η ανίσωση |χ|>-4 έχει λύσεις όλους τους αριθμούς αφού κάθε αριθμός έχει απόλυτη τιμή από 0 και πάνω.
Η ανίσωση |χ|>0 έχει λύση όλους τους αριθμούς εκτός το 0
Η ανίσωση
Η ανίσωση
Έτσι λοιπόν για να λύσεις την άσκηση που έχεις θα πρέπει να έχεις υπόψη σου αυτές τις δύο ιδιότητες (μια που έχει το < και μια που έχει το >) και πράττεις ανάλογα. Το κακό με την άσκησή σου είναι ότι δεν είναι μια ανίσωση αλλά είναι σύστημα δύο ανισώσεων και εμείς καλούμαστε να βρούμε τις κοινές τους λύσεις, δηλαδή τους αριθμούς που επαληθεύουν και τις δύο ανισώσεις:
Την πρώτη από αυτές θα τη λύσουμε με την πρώτη ιδιότητα και τη δεύτερη με τη δεύτερη ιδιότητα.
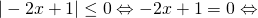
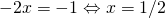 (κοίτα εδώ)
(κοίτα εδώ)
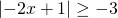 που ισχύει πάντα (αόριστη- κοίτα εδώ)
που ισχύει πάντα (αόριστη- κοίτα εδώ)
Έτσι λοιπόν για την πρώτη έχουμε:
Ενώ για τη δεύτερη έχουμε:
Η δεύτερη λοιπόν μας έδωσε ως λύσεις όλους τους αριθμούς και η πρώτη μόνο τον αριθμό 1/2 επομένως ο μόνος αριθμός που είναι λύση και της μιας και της άλλης είναι μόνο το 1/2.
Ο τρόπος με τον οποίο λύσαμε την άσκηση αυτή είναι στηνη ύλη της Α’ Λυκείου επειδή δεν ξέρω σε ποια τάξη πας αν θέλεις κάτι διαφορετικό μπορείς να μου στείλεις μήνυμα,
Υστερόγραφο: Συγνώμη για την καθυστερημένη απάντηση αλλά έλειπα διακοπές.
Το 3|χ+1|=2|χ-1| πως γινεται ?Αν μπορειτε να μου εξηγησεται γενικοτερα το πολλαπλασιασμο με τα απολυτα με αυτο το παραδειγμα.
Λάμπρο, απλώς ο αριθμός μπαίνει μέσα στο απόλυτο:
στη συνέχεια βγάζεις τα απόλυτα όπως αναφέρεται εδώ ή υψώνεις και τα δύο μέλη στο τετράγωνο:
και λύνεις δευτεροβάθμια εξίσωση. Όπου βρίσκεις λύσεις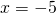 ή
ή 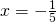
Ευχαριστω παρα πολυ κυριε Παναγιωτη.Με διευκολυνατε αφανταστα.Ευχαριστω και παλι .
Μπορειτε να μου δειξετε πως γινεται το |χ+2|+2χ=0 και το 3|χ+1|-2|χ-1|<|χ|-2 με χρησιμοποιηση πινακα προσημων ;Γιατι με εχει μπερδεψει παρα πολυ ο πινακας προσημων …
Αμαλία,
σου στέλνω ένα αρχείο με τις λύσεις γιατί δεν μπορώ στο site να φτιάξω πινακάκια δεν ξέρω τον τρόπο ακόμη.
Η καθηγητρια μας εδωσε το |3-π|+|4-π| και ειπε οτι η λυση ειναι =-3+π+4-π=1 και μας ειπε οτι το |3-π| ειναι αρνητικος και το |4-π| ειναι θετικος. πως γινεται αυτο?τι κανουμε?
Δημήτρη,
για να μπορέσεις α βγάλεις ένα απόλυτο θα πρέπει να ξέρεις τι πρόσημο έχει το περιεχόμενό του. Πιο συγκεκριμένα. επειδή το απόλυτο δεν μπορεί να είναι αρνητικός αριθμός (από τον ορισμό της απόλυτης τιμής) αν γνωρίζεις ότι το περιεχόμενο του απολύτου είναι θετικό τότε το διώχνεις και κρατάς μόνο το περιεχόμενο, για παράδειγμα το |7|=7. Ενώ όταν γνωρίζεις ότι το περιεχόμενο είναι αρνητικό, διώχνεις το απόλυτο και κρατάς το περιεχόμενο αλλά με αλλαγμένο πρόσημο π.χ. |-6|=-(-6)=6. (πιο αναλυτικά θα το βρείς εδώ:http://mathland.gr/archives/1905 κι εδω: http://mathland.gr/archives/331
Στη συγκεκριμένη άσκηση που έχεις να λύσεις θα πρέπει πρώτα απ’ όλα να θυμιθείς ότι ο αριθμός π είναι περίπου 3,14. Έτσι το 3-π είναι αρνητικός αριθμός αφού το π είναι μεγαλύτερο από το 3. Άρα σύμφωνα με τα παραπάνω θα βγεί από το απόλυτο με αλλαγμένα πρόσημα και θα έχεις |3-π|=-(3-π)=-3+π. Πάμε τώρα στο άλλο απόλυτο επειδή το 4-π είναι θετικό αφού το 4 είναι μεγαλύτερο από το π, θα βγει από το απόλυτο όπως είναι κι άρα |4-π|=4-π. Πάρε τώρα και τα δύο μαζί και θα έχεις ότι: |3-π|+|4-π|=-(3-π)+(4-π)=-3+π+4-π=4-3+π-π=1
euxaristw polu
Γεια σας μπορειτε να μου λυσετε δυο ασκησεις με απολυτες τιμες επειδη δν μπορω να τις λυσω?Λοιπον:
1) α) |-1-2|χ+2||
β) |-|2χ-1|-5|=|-|1-2χ|-7|
2) |2χ+3|+|χ-1|=|6+4χ|
Δημήτρη, κάνε κλικ στο σύνδεσμο που σου δίνω να κατεβάσεις τη λύση: Λύσεις
Πραγματικα δν 3ερω πως να σας ευχαριστησω τα κανετε αναλυτικα και ωραια μπραβο σας!Λοιπον οσον αφορα το α που 3εχασα το «=» μου 3εφυγε.Το σωστο ειναι: 1) α) |-1-2|χ+2||=9
Επισης ηθελα να σας ρωτησω αν χρειαζομαι βοηθεια και σε αλλες ασκησεις που περιεχουν απολυτες τιμες με κλασμα η με ριζα η καποια δυναμη αυτα ολα τα συμβολα υπαρχει καποιος χωρος να σας τα στειλω η οχι η να κατεβασω καποιο προγραμμα επειδη οπως 3ερετε μαθηματικα συμβολα απο το πληκτρολογιο δν γινετε?
Δημήτρη ρίξε μια ματιά σε αυτό: Πως γράφουμε μαθηματικά σύμβολα στο site και σε αυτό:http://www.codecogs.com/latex/eqneditor.php
2|3-x|-|2x+5|=0 ??
Χωρίζουμε τα απόλυτα και υψώνουμε στο τετράγωνο και τα δύο μέλη για να διώξουμε τα απόλυτα εκμεταλευώμενοι την ιδιότητα: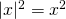
αντιμετωπιζω καποια δυσκολια..ενω καταλαβαινω ολα αυτα που λετε και τις λυσεις των ασκησεων δεν μπορω να λυσω αυτες που εχω..
μηπως ξερετε τι πρεπει να κανουμε σε αυτην εδω;
|χ στο τετραγωνο+2|-|-χ στο τετραγωνο+4χ-4|+4χ :/
εχω πολλαπλασιασει μονο τη δευτερη παρενθεση με το -1 και μου εχει βγει μια ταυτοτητα..χρησιμευει αυτο;
Βαλεντίνα κάθε φορά πρέπει να ψάχνεις μήπως μπορείς να ξέρεις το πρόσημο του περιεχομένου του απολύτου.
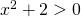 άρα
άρα 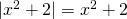
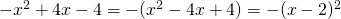 άρα
άρα 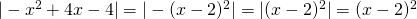 αφού
αφού 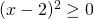
Στην άσκηση που μου γράφεις έχουμε:
οπότε:
Μπράβο Παναγιώτη δώσε γνώση απλόχερα
Αν |x|μικροτερο ίσο του 2 και |y|μικρότερο ίσο του 3 τοτε νδο:
|x+y| μικρότερο ίσο του 5
Αυτο πως λύνεται;
μπορειτε να μου λυσετε αυτην την ασκηση γτ δεn mporo?
-|2x-1|-1/4 =|1-2x|- |6x-3|-2/8 einai klasma alla den 3ero pos alliow na to kano..
Χριστίνα αν θες πες μου ο παρονομαστής 4 τι αριθμητή (ακριβώς) έχει το ίδιο και για τον παρονομαστή 8
φιλε πεστευω οτι εκανες λαθος στο -3-9=-4 ξερω οτι κανει -12
Οδυσσέα σε ευχαριστώ για την παρατήρηση, αλλά νομίζω ότι είναι σωστό γιατί λέει:
γεια σας εχω μια ασκηση την οποια δεν μπορω να λυσω ειναι η εξης :
f(x)= x^2-4/ 4-2|x-1|
να βρειτε το πεδιο ορισμου της
Ο παρονομαστής πρέπει να είναι διάφορος του μηδενός. Πρέπει λοιπόν να βρεις πότε αυτός μηδενίζεται και να αφαιρέσεις από το R, αυτούς τους αριθμούς. Για να δεις για ποιες τιμές του χ μηδενίζεται ο παρονομαστής λύνεις την εξίσωση:
πράγμα που μας δίνει δύο εκδοχές: είτε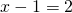 είτε
είτε 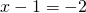 δηλαδή είτε
δηλαδή είτε 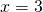 είτε
είτε 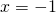 . Έτσι λοιπόν αφού ο παρονομαστής γίνεται ίσος με 0 όταν το χ πάρει την τιμή -1 ή την τιμή 3, το πεδίο ορισμού θα είναι όλοι οι πραγματικοί αριθμοί εκτός των -1 και 3. Δηλαδή
. Έτσι λοιπόν αφού ο παρονομαστής γίνεται ίσος με 0 όταν το χ πάρει την τιμή -1 ή την τιμή 3, το πεδίο ορισμού θα είναι όλοι οι πραγματικοί αριθμοί εκτός των -1 και 3. Δηλαδή 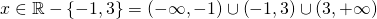
καλησπερα ..τι κανω οταν για παρανομαστη σε κλασμα εχω μια εξισωση δευτερου βαθμου σε απολυτο?
Πετάς το απόλυτο και λύνεις την εξίσωση κανονικά. Αφού βρεις τις λύσεις της εξίσωσης τις εξαιρείς απο το σύνολο των πραγματικών αριθμών. Αυτό γίνεται γιατί ισχύει |χ|=0 αν και μόνο αν χ=0, δηλαδή το απόλυτο είναι ίσο με το μηδέν μόνο στην περίπτωση που το περιεχόμενό του είναι ίσο με το μηδέν, άρα ασχολήσε μόνο με το περιεχόμενο του απολύτου.
/2x-3/=1 opoy/ apolyto