Εξίσωση 2ου βαθμού (ή δευτεροβάθμια εξίσωση) είναι η εξίσωση που περιέχει έναν άγνωστο (π.χ. τον x) και έχει ή μπορεί να πάρει τη μορφή ![]() με
με ![]() .
.
Όταν μας δώσουν μια εξίσωση για να βρούμε τις λύσεις της και δεν είναι στη παραπάνω μορφή δεν γνωρίζουμε αν πράγματι είναι δευτεροβάθμια εξίσωση ή όχι. Γι’ αυτό είμαστε υποχρεωμένοι να κάνουμε κάποια «προεργασία» ώστε να είμαστε σε θέση να αντιληφθούμε το βαθμό της εξίσωσης και κατόπιν να ψάξουμε να βρούμε τις λύσεις. Γιατί με άλλο τρόπο δουλεύουμε στις εξισώσεις πρώτου βαθμού, με άλλο σε αυτές που είναι δεύτερου βαθμού, διαφορετικά στις τριτοβάθμιες κ.ο.κ. Όσον αφορά στις πρωτοβάθμιες εξισώσεις έχουμε δώσει τη μεθοδολογία εδώ.
Η «προεργασία» λοιπόν που πρέπει να γίνει είναι ήδη γνωστή, θα πρέπει:
- να απαλλάξουμε την εξίσωση από τους παρονομαστές που τυχόν έχει
(πολλαπλασιάζοντας όλους τους όρους με το ΕΚΠ των παρονομαστών)
- να διώξουμε τις παρενθέσεις
(με χρήση της επιμεριστικής ιδιότητας) και τέλος - να κάνουμε αναγωγή όμοιων όρων
(να «συμμαζέψουμε» την εξίσωση προσθέτοντας μεταξύ τους τους όμοιους όρους)
Σε αυτό το σημείο είμαστε σε θέση να δούμε το βαθμό της εξίσωσης και αν
- ο άγνωστος δεν είναι υψωμένος σε καμία δύναμη, τότε έχουμε να λύσουμε μια πρωτοβάθμια εξίσωση κατά τα γνωστά (χωρίζουμε γνωστούς – άγνωστους κ.τ.λ.)
- η μεγαλύτερη δύναμη στην οποία εμφανίζεται ο άγνωστος είναι το τετράγωνο, τότε είμαστε στη περίπτωση της δευτεροβάθμιας εξίσωσης και η διαδικασία που ακολουθούμε για να βρούμε τις λύσεις είναι η παρακάτω:
- Μεταφέρουμε όλους τους όρους στο ένα μέλος ώστε η εξίσωση να πάρει τη μορφή
![Rendered by QuickLaTeX.com \[\alpha\chi^2+\beta\chi+\gamma=0\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-81ace40d7c80db6a6ba0536fc9fb3af2_l3.png)
- Ξεκαθαρίζουμε ποιοι αριθμοί παίζουν το ρόλο των α, β και γ (α: ο συντελεστής του χ2, β: ο συντελεστής του χ και γ ο σταθερός όρος).
- Με τη βοήθεια των α, β, γ και του τύπου
![Rendered by QuickLaTeX.com \[\Delta=\beta^2-4\alpha\gamma\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-5d415ece8e5ba7b1aecd03b1a3fc7504_l3.png)
υπολογίζουμε ένα νέο αριθμό τον Δ που λέγεται «Διακρίνουσα» (διάβασε το Σχόλιο1 παρακάτω)
- Από το «είδος» αυτού του αριθμού, του Δ, εξαρτάται κα το πως θα προχωρήσουμε παρακάτω. Και πιο συγκεκριμένα:
- αν η Διακρίνουσα (Δ) είναι αρνητικός αριθμός, τότε η εξίσωση μας δεν έχει λύσεις, είναι όπως λέμε σε τέτοιες περιπτώσεις αδύνατη
- αν η Διακρίνουσα (Δ) είναι θετικός αριθμός, τότε η εξίσωση έχει 2 λύσεις διαφορετικές μεταξύ τους και που τις υπολογίζουμε από τους τύπους
![Rendered by QuickLaTeX.com \[\chi_1=\frac{-\beta-\sqrt{\Delta}}{2\alpha}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-69010efac1192b69e8f519e706b5b494_l3.png)
και
![Rendered by QuickLaTeX.com \[\chi_2=\frac{-\beta+\sqrt{\Delta}}{2\alpha}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-d821ee0f34f5ff8251b1eb2d5d5dca16_l3.png)
(διάβασε το Σχόλιο2)
- αν η Διακρίνουσα (Δ) είναι ίση με 0, τότε η εξίσωση έχει δύο ίσες λύσεις (ή όπως συνήθως λέμε μια διπλή λύση) που μπορούμε να υπολογίσουμε από τον τύπο
![Rendered by QuickLaTeX.com \[\chi_1=\chi_2=\frac{-\beta}{2\alpha}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-d0834493947d83842b3e5b8053d83815_l3.png)
(Σχόλιο3)
Συνοπτικά η διαδικασία που ακολουθούμε ώστε να βρούμε τις λύσεις σε μια εξίσωση της μορφής
![]()
καθώς και οι περιπτώσεις που μπορούν να προκύψουν φαίνονται στο σχήμα που ακολουθεί:
Λυμένα παραδείγματα για να κατανοήσουμε καλύτερα αυτά που αναφέραμε θα δείτε στο επόμενο άρθρο.
Η παράσταση ![]() συμβολίζεται με Δ και λέγεται «Διακρίνουσα». Η ονομασία δεν είναι τυχαία γιατί η διακρίνουσα μας βοηθάει να διακρίνουμε το πλήθος των ριζών (λύσεων) της εξίσωσης. Πράγματι,
συμβολίζεται με Δ και λέγεται «Διακρίνουσα». Η ονομασία δεν είναι τυχαία γιατί η διακρίνουσα μας βοηθάει να διακρίνουμε το πλήθος των ριζών (λύσεων) της εξίσωσης. Πράγματι,
- Δ<0
 0 λύσεις
0 λύσεις - Δ=0
 1 λύση διπλή
1 λύση διπλή - Δ>0
 2 λύσεις διαφορετικές
2 λύσεις διαφορετικές
Οι δύο αυτοί τύποι μπορούν να γραφούν σε έναν πιο συμμαζεμένο:
![]()
Στην πραγματικότητα ο τύπος αυτός δεν είναι κάποιος νέος τύπος που πρέπει να απομνημονεύσουμε αρκεί να ξέρουμε απ’ έξω τον προηγούμενο τύπο αφού από εκεί προκύπτει και αυτός μόνο που τώρα το Δ είναι 0. Πράγματι,
![]()


ευχαριστώ με βοήθησαν πολύ……….
Ειμαι γενικα εξυπνος καταλαβαίνω τα μαθηματικά απλα καποια ετσι οπως τα λεει το βιβλιο και ετσι οπως ειναι και ο καθηγητής μας……Εγω επειδη βοηθηθηκα πολλοι θα συμβουλευσω τους συμμαθητες μου να μπαινουν εδω και να ριχνουν καμια ματια……..Ευχαριστω και για την θεωρια πολυ καλογραμενη
μια ερωτηση…στο βιβλιο της α΄ λυκειου στις εξισωσεις 2ου βαθμου εχει μια ασκηση που δεν μπορω να λυσω…
….να βρειτε τις τιμες του αΕR για τις οποιες η εξισωση εχει διπλη ριζα
Ανδρέα, όπως θα διάβασες και στο άρθρο παραπάνω μια εξίσωση δεύτερου βαθμού για να λυθεί πρέπει να έρθει στη μορφή: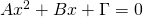 . Το πλήθος των λύσεων που έχει αυτή η εξίσωση καθορίζεται από την Διακρίνουσα
. Το πλήθος των λύσεων που έχει αυτή η εξίσωση καθορίζεται από την Διακρίνουσα 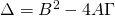 . Για να έχει αυτή η εξίσωση μια διπλή ρίζα ε’ιναι απαραίτητο η Διακρίνουσά της να είναι ίση με το 0. Άρα εμείς θα πρέπει να βρούμε για ποιες τιμές του α η Διακρίνουσα γίνεται ίση με 0. Υπολογίζουμε λοιπόν την Διακρίνουσα της εξίσωσής μας ως εξής: A=2, B= α – 9 και Γ=
. Για να έχει αυτή η εξίσωση μια διπλή ρίζα ε’ιναι απαραίτητο η Διακρίνουσά της να είναι ίση με το 0. Άρα εμείς θα πρέπει να βρούμε για ποιες τιμές του α η Διακρίνουσα γίνεται ίση με 0. Υπολογίζουμε λοιπόν την Διακρίνουσα της εξίσωσής μας ως εξής: A=2, B= α – 9 και Γ=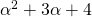 , οπότε
, οπότε
Επειδή όπως προαβαφέραμε πρέπει να βρούμε πότε η Διακρίνουσα είναι ίση με το 0 γι ‘αυτό το λόγο λύνουμε την εξίσωση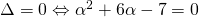 κι έχουμε: Α=1, Β=6 και Γ=-7 άρα
κι έχουμε: Α=1, Β=6 και Γ=-7 άρα
κι επομένως
δηλαδή,
Απάντηση: Για να έχει η εξίσωση μια διπλή ρίζα πρέπει το α να είναι ή -7 ή 1.
otan h diakrinousa einai 8etikh briskw tis rizes k tis grafw (x-x1)(x-x2) swsta?????otan einai D=0 pws grafw thn rizaaa???
Αυτό που λες το κάνεις (με μια μικρή διόρθωση) όχι όταν θες να λύσεις την εξίσωση αλλά όταν θέλεις να μετατρέψεις το τριώνυμο σε γινόμενο (να κάνεις παραγοντοποίηση δηλαδή).
Στην περίπτωση αυτή έχουμε:
Αναλυτικά μπορείς να τα διαβάσεις εδώ
geia sas! prospa8w na liso mia askisi kai xriazome voi8ia.. 16x sto tetragono + x= 0
Η εξίσωση αυτή μπορεί να λυθεί με παραγοντοποίηση ώστε από δεύτερου βαθμού που είναι να καταλήξει σε δύο εξισώσεις πρώτου βαθμού (διάβασε κι αυτό).
Βγάζεις λοιπόν κοινό παράγοντα το χ
κι επειδή τώρα έχεις ένα γινόμενο που κάνει μηδέν είναι σίγουρο ότι κάποιος από τους παράγοντές του θα είναι ‘ισος με μηδέν.
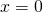 ή
ή 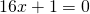
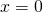 ή
ή 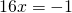
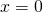 ή
ή 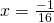
Επίσης αν το έχεις διδαχθεί στο σχολείο μπορείς να την λύσεις και με την βοήθεια των τύπων που θα βρείς εδώ ακολουθώντας τη διαδικασία που περιγράφεται στο άρθρο.
πως λυνετε αυτη η ασκηση: δινεται εξισωση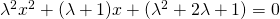 βρειτε τον λ ωστε η παραπανω εξισωση να εχει : α) ριζες αντιθετες Β)ριζεσ αντιστροφεσ
βρειτε τον λ ωστε η παραπανω εξισωση να εχει : α) ριζες αντιθετες Β)ριζεσ αντιστροφεσ
Βίβιαν, και για τα δύο ερωτήματα θέλουμε η εξίσωση να έχει δύο λύσεις τη μια φορά αντίθετες και την άλλη αντίστροφες. Από αυτό καταλαβαίνουμε ότι η εξίσωση που έχουμε είναι δεύτερου βαθμού κι επομένως ο συντελεστής του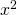 δεν είναι μηδέν, δηλαδή ισχύει
δεν είναι μηδέν, δηλαδή ισχύει 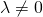 . Πάμε τώρα στα ερωτήματα
. Πάμε τώρα στα ερωτήματα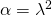 και
και 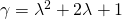 . Επομένως θα έχουμε:
. Επομένως θα έχουμε:
Α) Για να είναι οι δύο ρίζες αντίθετες θα πρέπει να έχουν άθροισμα ίσο με μηδέν (σου θυμίζω δύο αριθμοί λέγονται αντίθετοι όταν το άθροισμά τους είναι ίσο με 0). Όμως το άθροισμα των ριζών του τριωνύμου (συμβολίζεται με S) ξέρουμε από τη θεωρία (τύποι Vieta) ότι είναι ίσο με -β/α. Θα πρέπει λοιπόν να ισχύει:
-β/α=0 συνεπώς θα πρέπει να είναι β=0 όμως στην εξίσωσή σου το ρόλο του β παίζει το λ+1. Άρα θα πρεπει να είναι λ+1=0 ή αλλιώς λ=-1′
Β) Όμοια για να είναι οι ρίζες αντίστροφες θα πρέπει το γινόμενό τους να είναι ίσο με 1. Γιατί αντίστροφοι λέγονται δύο αριθμοί όταν το γινόμενό τους είναι ίσο με 1. Το γινόμενο των ριζών όμως πάλι από τους τύπους Vieta είναι ίσο με γ/α. Θα πρέπει λοιπόν να ισχύει: γ/α=1 δηλαδή γ=α. Στην συγκεκριμένη εξίσωση το
ευχαριστω πολυ για την απαντηση σας στο προηγουμενο ερωτημα μου! αυτη τη φορα θελω βοηθεια σε αυτη την ασκηση! οπου 2 και 3 μετα απο χ και χ1 και χ2 και λ ειναι τετραγωνα και κυβοι!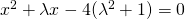
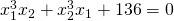
δινεται η εξισωση
α) να αποδειχθει οτι η παραπανω εξισωση για καθε λ Ε R εχει 2 ανισες ριζεσ
β)αν χ1 και χ2 οι ριζεσ τησ, να βρεθει ο λ ωστε
α)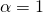 ,
, 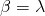 ,
, 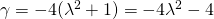
κι αφού η διακρίνουσα είναι μονίμως θετική η εξίσωση έχει 2 λύσεις άνισες για οποιαδήποτε τιμή του λ.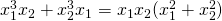 (σχέση 1)
(σχέση 1)
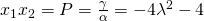
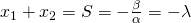 άρα:
άρα: 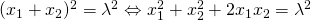
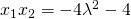 κι επομένως:
κι επομένως:
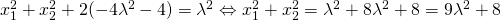
β)
Όμως:
από το προηγούμενο όμως έχουμε ότι
Γυρίζουμε λοιπόν τώρα στη σχέση 1 κι έχουμε:
Θέλουμε τώρα να λύσουμε την εξίσωση: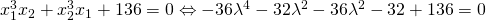 που μετά από τις πράξεις φτάνει εδώ:
που μετά από τις πράξεις φτάνει εδώ: 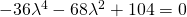
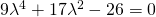
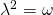 και
και 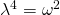 .
.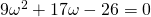 που μας δίνει λύσεις το 1 και μια αρνητική που δεν την δεχόμαστε γιατί σαν ω έχουμε θέσει το
που μας δίνει λύσεις το 1 και μια αρνητική που δεν την δεχόμαστε γιατί σαν ω έχουμε θέσει το 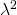 κι επομένως δεν μπορεί να είναι αρνητικό. Έχουμε φτάσει επομένως στό ότι
κι επομένως δεν μπορεί να είναι αρνητικό. Έχουμε φτάσει επομένως στό ότι 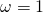 δηλαδή
δηλαδή 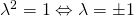
διαρούμε με το -4 για να έχουμε μικρότερους αριθμούς και καταλήγουμε σε αυτή την εξίσωση:
η οποία για να λυθεί χρειάζεται να θέσουμε όπου
Λύνουμε λοιπόν την:
Γεια σας! Μήπως θα μπορούσατε να μου δώσετε απάντηση στο πώς λύνεται η εξής δευτεροβάθμια εξίσωση;;;
2x(εις την δευτέρα) + x + 5 = 0
άρα: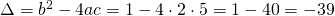
Επειδή η διακρίνουσα είναι αρνητική η εξίσωση είναι αδύνατη.
Δίνεται η εξίσωση x2 + 2λx + λ – 2 = 0 , με παράμετρο λ∈ℝ
α) Να βρείτε τη διακρίνουσα της εξίσωσης.
β) Να αποδείξετε ότι η παραπάνω εξίσωση έχει ρίζες πραγματικές και άνισες για κάθε λ∈ℝ.
γ) Αν 1 2 x , x είναι οι ρίζες της παραπάνω εξίσωσης, τότε να βρείτε για ποια τιμή του λ ισχύει:
1 2 1 2 x + x = −x ⋅ x
Μπορειτε να μου πειτε πως λυνεται?
όμως ισχύει:
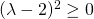 άρα
άρα 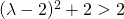 , δηλαδή η διακρίνουσα είναι μεγαλύτερη του 2, ανεξάρτητα από την τιμή του λ, πράγμα που σημαίνει ότι είναι πάντα θετική κι έτσι η εξίσωση έχει ρίζες πραγματικές και άνισες.
, δηλαδή η διακρίνουσα είναι μεγαλύτερη του 2, ανεξάρτητα από την τιμή του λ, πράγμα που σημαίνει ότι είναι πάντα θετική κι έτσι η εξίσωση έχει ρίζες πραγματικές και άνισες.
Γεια σας θα μπορούσατε να με βοηθήσετε με την παρακάτω δευτεροβάθμια εξίσωση??? χ²+4χ=5
Πρέπει να φέρεις όλους τους όρους στο πρώτο μέλος: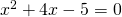 και στη συνέχεια να εφαρμόσεις τους τύπους.
και στη συνέχεια να εφαρμόσεις τους τύπους.
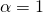
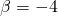 και
και 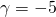 άρα
άρα 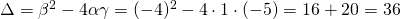
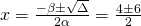 δηλαδή
δηλαδή 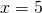 ή
ή 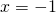
επομένως αφού η διακρίνουσα είναι θετική θα έχει η εξίσωση δύο διαφορετικές λύσεις τις:
Γεια σας! Δεν μπορω να καταλαβω τι γινεται με το S,P ! ουτε το βιβλιο με βοηθαει ουτε η καθηγητρια … γινετε να κανουμε κατι στην προκειμενη περιπτωση? (Τη Δευτερα δινω αλγεβρα , οποτε απαντηστε οσο πιο γρηγορα μπορειτε και αν μπορειτε παρακαλω)! Ευχαριστω για το χρονο σας!
Καλησπέρα! Σε μελέτη συνάρτησης όπου Δ<0, λέμε ότι είναι αδύνατη. Συνεχίζουμε μετά κανονικά να βρούμε κυρτότητα; Σκέφτομαι ότι όταν μια συνάρτηση είναι αδύνατη, τότε και η καμπύλη που την απεικονίζει δεν υπάρχει. Άρα ποιος ο λόγος να βρω κυρτότητα σε μια ανύπαρκτη καμπύλη;
Να σημειώσω ότι η λύση της πρέπει να γίνει αποκλειστικά με πραγματικούς αριθμούς…
Ευχαριστώ εκ των προτέρων!
Μίνα, δεν ακριβώς έτσι τα πράγματα όπως τα φαντάζεσαι. Όταν μελετάς μια συνάρτηση (ας την πούμε f) ως προς την κυρτότητα κάνεις τα παρακάτω: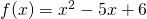 τότε η πρώτη παράγωγος της είναι η
τότε η πρώτη παράγωγος της είναι η 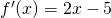 και η δεύτερη παράγωγος είναι
και η δεύτερη παράγωγος είναι 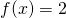 . Βλέπυμε λοιπόν ότι η δεύτερη παράγωγος είναι ίση με 2 δηλαδή πάντα θετική και συμπεραίνουμε ότι η συνάρτηση στρέφει τα κοίλα προς τα πάνω.
. Βλέπυμε λοιπόν ότι η δεύτερη παράγωγος είναι ίση με 2 δηλαδή πάντα θετική και συμπεραίνουμε ότι η συνάρτηση στρέφει τα κοίλα προς τα πάνω.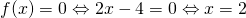 . Όπως είπαμε προηγούμενα το πρόσημο της αλλάζει (αν αλλάζει) εκεί που είναι η ρίζα της στο συγκεκριμένο παράδειγμα στο 2. Βάζεις λοιπόν δύο τιμές στη θέση του χ στο τύπο της δεύτερης παραγώγου μία μεγαλύτερη του 2 (όπως έκανα εγώ παραπάνω που έβαλα το 10) και βλέπεις ότι το αποτέλεσμα είναι θετικό και άρα για κάθε χ μεγαλύτερο του 2 η συνάρτηση στρέφει τα κοίλα προς τα πάνω, βάζεις και μια τιμή μικρότερη του 2 (εγώ τυχαία έβαλα το 1) και παρατηρείς ότι το αποτέλεσμα είναι αρνητικό οπότε η f στρέφει τα κοίλα κάτω για κάθε χ μικρότερο του 2.
. Όπως είπαμε προηγούμενα το πρόσημο της αλλάζει (αν αλλάζει) εκεί που είναι η ρίζα της στο συγκεκριμένο παράδειγμα στο 2. Βάζεις λοιπόν δύο τιμές στη θέση του χ στο τύπο της δεύτερης παραγώγου μία μεγαλύτερη του 2 (όπως έκανα εγώ παραπάνω που έβαλα το 10) και βλέπεις ότι το αποτέλεσμα είναι θετικό και άρα για κάθε χ μεγαλύτερο του 2 η συνάρτηση στρέφει τα κοίλα προς τα πάνω, βάζεις και μια τιμή μικρότερη του 2 (εγώ τυχαία έβαλα το 1) και παρατηρείς ότι το αποτέλεσμα είναι αρνητικό οπότε η f στρέφει τα κοίλα κάτω για κάθε χ μικρότερο του 2.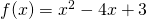 βρίσκεις τις ρίζες που είναι το 1 και το 3 και δοκιμάζεις: έναν αριθμό μεγαλύτερο του 3 και βλέπεις ότι το αποτέλεσμα βγαίνει θετικό, μετά δοκιμάζεις έναν αριθμό μεταξύ του 1 και του 3 και βλέπεις ότι το αποτέλεσμα βγαίνει αρνητικό ενώ δοκιμάζοντας έναν αριθμό μικρότερο του 1 το αποτέλεσμα θα σου βγει θετικό. Άρα για κάθε χ μικρότερο του 1 ή μεγαλύτερο του 3 η συνάρτηση στρέφει τα κοίλα πάνω ενώ για οποιοδήποτε χ μεταξύ 1 και 3 στρέφει τα κοιλα κάτω.
βρίσκεις τις ρίζες που είναι το 1 και το 3 και δοκιμάζεις: έναν αριθμό μεγαλύτερο του 3 και βλέπεις ότι το αποτέλεσμα βγαίνει θετικό, μετά δοκιμάζεις έναν αριθμό μεταξύ του 1 και του 3 και βλέπεις ότι το αποτέλεσμα βγαίνει αρνητικό ενώ δοκιμάζοντας έναν αριθμό μικρότερο του 1 το αποτέλεσμα θα σου βγει θετικό. Άρα για κάθε χ μικρότερο του 1 ή μεγαλύτερο του 3 η συνάρτηση στρέφει τα κοίλα πάνω ενώ για οποιοδήποτε χ μεταξύ 1 και 3 στρέφει τα κοιλα κάτω.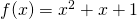 η οποία έχει διακρίνουσα αρνητική κι επομένως δεν έχει ρίζες (αδύνατη όπως λες) αυτό σημαίνει ότι δεν αλλάζει πρόσημο δηλαδή για κάθε τιμή του χ θα έχει πάντα το ίδιο πρόσημο. Πως το βρίσκεις αυτό; και πάλι με δοκιμή: βάζεις μια οποιαδήποτε τιμή στο χ έστω το 1 που είναι εύκολο και βλέπεις ότι η δεύτερη παράγωγος βγαίνει 3, θετική άρα η συνάρτηση f θα στρέφει σε όλο το πεδίο ορισμού της για οποιοδήποτε χ τα κοίλα προς τα πάνω.
η οποία έχει διακρίνουσα αρνητική κι επομένως δεν έχει ρίζες (αδύνατη όπως λες) αυτό σημαίνει ότι δεν αλλάζει πρόσημο δηλαδή για κάθε τιμή του χ θα έχει πάντα το ίδιο πρόσημο. Πως το βρίσκεις αυτό; και πάλι με δοκιμή: βάζεις μια οποιαδήποτε τιμή στο χ έστω το 1 που είναι εύκολο και βλέπεις ότι η δεύτερη παράγωγος βγαίνει 3, θετική άρα η συνάρτηση f θα στρέφει σε όλο το πεδίο ορισμού της για οποιοδήποτε χ τα κοίλα προς τα πάνω.
Πρώτα βρίσκεις την πρώτη παράγωγο της συνάρτησης (που την συμβολίζουμε με f΄ ).
Μετά βρίσκεις την δεύτερη παράγωγο της συνάρτησης (δηλαδή την παράγωγο της παραγώγου αυτή συμβολίζεται με f΄΄ )
Αυτό που σε ενδιαφέρει τώρα είναι το πρόσημο της δεύτερης παραγώγου, δηλαδή πότε (για ποιες τιμές της μεταβλητής χ) η f΄΄ είναι θετική και πότε αρνητική και αυτό γιατί αν γνωρίζεις ότι η δεύτερη παράγωγος είναι θετική συμπεραίνεις ότι η συνάρτηση f που μελετάς στρέφει τα κοίλα προς τα πάνω ενώ σε αντίθετη περίπτωση (f΄΄ αρνητική) στρέφει τα κοίλα κάτω.
Πως όμως βρίσκεις το πρόσημο της δεύτερης παραγώγου;
Βάζεις τη δεύτερη παράγωγο ίση με το 0 και λύνεις την εξίσωση f΄΄ = 0 και αυτό γιατί το πρόσημο αλλάζει συνήθως εκεί που μηδενίζεται δηλαδή στις ρίζες της f΄΄. Αν τώρα τυχαίνει να μην έχει ρίζες συμπεραίνουμε ότι η δεύτερη παράγωγος είναι μονίμως και για οποιαδήποτε τιμή του χ θετική ή μόνιμα αρνητική, δηλαδή όπως λέμε διατηρεί σταθερό πρόσημο. κι έτσι η η συνάρτηση που μελετάς θα στρέφει συνεχώς τα κοίλα προς τα πάνω ή συνέχεια προς τα κάτω.
Θα σου δώσω μερικά παραδείγματα για να γίνω λίγο πιο συγκεκριμένος.
1. Έστω
2. Έστω μια συνάρτηση f τώρα που έχει ως δεύτερη παράγωγο την f΄΄(x)= 2x – 4. Αυτή δεν διατηρεί σταθερό πρόσημο αλλά εξαρτάται από τι τιμή θα πάρει το x. Για παράδειγμα όταν το x = 10, f΄΄(10) =20 – 4 = 16 ενώ όταν x = 1 f΄΄(1) = -2. Για να βρούμε λοιπόν το πότε είναι θετική και πότε αρνητική η f΄΄ λύνουμε την εξίσωση
3. Αν μια συνάρτηση f έχει
4. Αν τώρα μια συνάρτηση f έχει δεύτερη παράγωγο την
Ελπίζω να σε βοήθησα, αν έχεις ακόμη απορίες μπορείς να με ξαναρωτήσεις.
SOS !!! θα μπορούσε κάποιος να με βοηθήσει να λύσω εξισώσεις 2 βαθμού όπως:
1) Δίνεται η εξίσωση χ στη δευτέρα -(2 λ+1)χ + λ=0 α) Να δείξετε ότι η εξίσωση έχει 2 άνισες πραγματικές ρίζες για κάθε λ ανήκει R. β) Αν χ1, χ2 οι ρίζες της εξίσωσης, να βρείτε για ποια τιμή του λ ισχύει χ1+χ2=4χ1χ2-λ.
2) Δίνεται η εξίσωση χ στη δευτέρα-(λ στη δευτέρα +5)χ +18=0.Αν η εξίσωση έχει δύο ρίζες , όπου μία ρίζα είναι διπλάσια της άλλης, τότε να βρείτε τις ρίζες και την τιμή του λ.
3) Να βρείτε τις τιμές του λ ώστε η μία ρίζα της εξίσωσης χ στη δευτέρα -6 χ +3 λ=0 να είναι το τετράγωνο της άλλης .
4) Να βρείτε την τιμή του λ ώστε οι ρίζες της εξίσωσης χ στη δευτέρα – λ χ -λ-5=0 να ικανοποιούν την σχέση: Χ1 στη δευτέρα – Χ1Χ2+Χ2 στη δευτέρα =19
Σας Ευχαριστώ!!
1) Για να έχει η εξίσωση 2 άνισες πραγματικές ρίζες θα πρέπει η Διακρίνουσά της να είναι θετική. Όμως η Διακρίνουσα της είναι η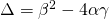 με
με 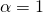 ,
, 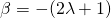 ,
, 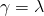 , άρα η διακρίνουσα είναι
, άρα η διακρίνουσα είναι 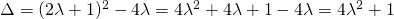 . Βλέπουμε λοιπόν ότι η Δ είναι πάντα θετική πράγμα που σημαίνει ότι η εξίσωση θα έχει 2 άνισες λύσεις.
. Βλέπουμε λοιπόν ότι η Δ είναι πάντα θετική πράγμα που σημαίνει ότι η εξίσωση θα έχει 2 άνισες λύσεις.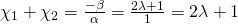 ενώ το γινόμενο των ριζών
ενώ το γινόμενο των ριζών 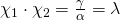 . Έτσι λοιπόν η σχέση που μας έχουν δώσει γίνεται:
. Έτσι λοιπόν η σχέση που μας έχουν δώσει γίνεται:
β)Από τη θεωρία γνωρίζουμε ότι το άθροισμα των ριζών
Λύνουμε τώρα την εξίσωση αυτή (άγνωστος είναι το λ) και βρίσκουμε:
2) Ας υποθέσουμε ότι η μια ρίζα η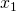 είναι η μικρότερη ρίζα ενώ η άλλη, η
είναι η μικρότερη ρίζα ενώ η άλλη, η 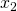 είναι η μεγαλύτερη αυτή που είναι διπλάσια από την άλλη. Άρα θα ισχύει:
είναι η μεγαλύτερη αυτή που είναι διπλάσια από την άλλη. Άρα θα ισχύει: 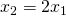 . Γνωρίζουμε από τη θεωρία ότι για το άθροισμα των ριζών ισχύει:
. Γνωρίζουμε από τη θεωρία ότι για το άθροισμα των ριζών ισχύει:
ενώ για το γινόμενο των ριζών ισχύει:
άρα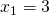 ή
ή 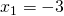 .
.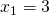 τότε θα είναι
τότε θα είναι 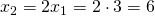 ενω το λ θα είναι
ενω το λ θα είναι 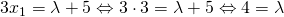 .
.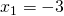 , το
, το 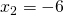 και το
και το 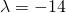
Όμως αν το
Στην περίπτωση που το
3) Αν είναι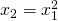 θα ισχύει:
θα ισχύει:
και
. Από την πρώτη εξίσωση βρίσκουμε ότι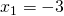 ή
ή 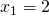 , οπότε από τη δεύτερη εξίσωση βρίσκουμε το λ,
, οπότε από τη δεύτερη εξίσωση βρίσκουμε το λ,
ή
4)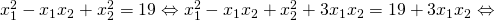
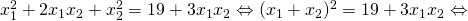

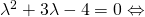
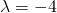 ή
ή 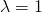
θα μπει στις εξετασεις και θελω βοηθεια πως λυνεται.
»Δινεται η εξισωση x2+λχ-λ+3=0.
Να βρεθουν οι τιμες του λ για τις οποιες η εξισωση:
α) εχει 1 διπλη ριζα
β) εχει 2 ριζες ανισες
γ) είναι αδυνατη.
Είναι εξίσωση 2ου βαθμού και θα βρούμε την Διακρίνουσα: α=1, β=λ, γ=-λ+3
Παρατηρούμε ότι η Διακρίνουσα είναι πολυώνυμο 2ου βαθμού, και για να απαντήσουμε στα παρακάτω ερωτήματα θα πρέπει να βρούμε τη σχέση της με το 0. Δηλαδή πότε η Διακρίνουσα γίνεται 0, πότε θετική και πότε αρνητική. Και αυτό γιατί σύμφωνα με τη θεωρία ισχύουν:
1 διπλή ρίζα αν και μόνο αν Δ=0,
2 ρίζες άνισες αν και μόνο αν Δ>0 και τέλος
αδύνατη αν και μόνο αν Δ<0
Λύνουμε λοιπόν την εξίσωση Δ=0
α=1, β=4, γ=-12
άρα οι ρίζες της Διακρίνουσας είναι: λ=-6, λ=2
(α) Για να έχει μια διπλή ρίζα πρέπει η Διακρίνουσα να είναι ίση με 0, αρα το λ πρέπει να είναι ίσο με -6 ή 2
(β) Για να έχει η εξίσωση 2 ρίζες άνισες θα πρέπει η Διακρίνουσα να είναι θετική. Αυτό συμβαίνει όταν το λ παίρνει τιμές έξω από το διάστημα των ριζών θα πρέπει λοιπόν το λ να είναι είτε μικρότερο του -6 είτε μεγαλύτερο του 2 (λ< -6 ή λ>2)
(γ) Για να είναι αδύνατη πρέπει το λ να παίρνει τιμές στο διάστημα ανάμεσα στις ρίζες δηλαδή να ισχύει -6<λ<2.
Γεια σας μηπως θα μπορουσατε να με βοηθησετε με την παρακάτω εξίσωση χ^2 + 2χ = 10 – y.
i) να βρουμε το χ οταν το y=0
ii) να βρουμε το y οταν το χ =0
Ευχαριστω εκ των προτερων