Κατ’ αρχάς να ξεκινήσουμε από τον τίτλο του άρθρου που είναι λάθος, γιατί αυτό που θα δούμε σ αυτή τη δημοσίευση είναι η διαδικασία που ακολουθούμε ώστε να βρούμε τη λύση μιας εξίσωσης 1ου βαθμού και αυτή (η διαδικασία) λέγεται επίλυση κι όχι λύση (το τι είναι λύση το έχουμε γράψει εδώ).
Ας δούμε λοιπόν ποια βήματα πρέπει να ακολουθούμε ώστε να βρίσκουμε σε οποιαδήποτε εξίσωση 1ου βαθμού, αν έχει λύση και ποια είναι αυτή ή αν δεν έχει λύσεις (αδύνατη). Σκοπός μας είναι μέσα από τη διαδικασία που θα ακολουθήσουμε, σε οποιαδήποτε πρωτοβάθμια εξίσωση κι αν μας έχει δοθεί, να καταλήξουμε στη πιό απλή μορφή εξίσωσης που υπάρχει και είναι αυτή:
![]() , όπου το
, όπου το ![]() και το
και το ![]() μπορεί να είναι οποιοσδήποτε αριθμός
μπορεί να είναι οποιοσδήποτε αριθμός
Με τέσσερα απλά βήματα (στη χειρότερη περίπτωση) μπορούμε να καταλήξουμε στη μορφή ![]() . Τα βήματα είναι τα παρακάτω που θα τα δούμε λύνοντας ταυτόχρονα κι ένα παράδειγμα:
. Τα βήματα είναι τα παρακάτω που θα τα δούμε λύνοντας ταυτόχρονα κι ένα παράδειγμα:
Βήμα 1ο:
Διώχνουμε τους παρονομαστές,
για να διώξουμε τους παρονομαστές από μια εξίσωση, πολλαπλασιάζουμε όλους τους όρους της εξίσωσης με το Ε.Κ.Π. των παρονομαστών.(περισσότερα θα βρείτε εδώ)
πολλαπλασιάσαμε με 6, γιατί ΕΚΠ(2,3,6)=6 |
Βήμα 2ο:
Διώχνουμε τις παρενθέσεις
Αν η εξίσωσή μας έχει παρενθέσεις (και να μην έχει είναι πολύ πιθανό να προκύψουν από το προηγούμενο βήμα), τότε τις διώχνουμε με σκοπό να ελευθερώσουμε τον άγνωστο που είναι φυλακισμένος μέσα σε αυτές. Οι παρενθέσεις φεύγουν με τη χρήση της επιμεριστικής ιδιότητας: ![]()
|
κάναμε επιμεριστική: 12(x+1)=12x+12 |
Βήμα 3ο:
Χωρίζουμε τους γνωστούς από τους άγνωστους όρους
Αφού διώξαμε και τις παρενθέσεις θα πρέπει να αρχίσουμε να κάνουμε προσθέσεις και αφαιρέσεις. Όμως πρόσθεση και αφαίρεση γίνεται μόνο σε όμοια πράγματα (αριθμοί με αριθμούς και άγνωστοι με άγνωστους) γι’ αυτό το λόγο αναγκαζόμαστε να μεταφέρουμε όλους τους αριθμούς(=γνωστοί) στο ένα μέλος και όλους τους άγνωστους όρους στο άλλο. Εδώ χρειάζεται προσοχή γιατί όποιος όρος αλλάζει μέλος, αλλάζει και πρόσημο.
|
όταν κάποιος όρος αλλάζει μέλος αλλάζει και πρόσημο |
Βήμα 4ο:
Συμμαζεύουμε 1ο και 2ο μέλος (αναγωγή όμοιων όρων)
Τώρα είμαστε σε θέση να κάνουμε πράξεις στο πρώτο και δεύτερο μέλος κι έτσι να καταλήξουμε στη μορφή:
![]()
|
α = 8 και β = 16 |
Τελικό Βήμα:
Μέχρι εδώ είδαμε ότι κάθε πρωτοβάθμια εξίσωση με 4 απλές κινήσεις καταλήγει στη μορφή ![]() . Τι γίνεται όμως από ‘δω και πέρα; Εδώ απλώς δίνουμε την απάντησή μας η οποία όμως εξαρτάται από τους αριθμούς
. Τι γίνεται όμως από ‘δω και πέρα; Εδώ απλώς δίνουμε την απάντησή μας η οποία όμως εξαρτάται από τους αριθμούς ![]() και
και ![]() που βρήκαμε παραπάνω και αυτό γιατί,
που βρήκαμε παραπάνω και αυτό γιατί,
- αν
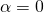 και
και 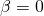 ,
,
η εξίσωσή μας θα έχει τη μορφή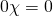 που είναι αόριστη αφού κάθε αριθμός την επαληθεύει.
που είναι αόριστη αφού κάθε αριθμός την επαληθεύει. - αν
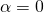 και
και 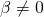 ,
,
η εξίσωσή μας θα έχει τη μορφή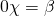 που είναι αδύνατη αφού είναι αδύνατον να βρεθεί αριθμός που αν πάρει τη θέση του
που είναι αδύνατη αφού είναι αδύνατον να βρεθεί αριθμός που αν πάρει τη θέση του 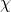 να μας δώσει μια σωστή ισότητα (θα προκύψει 0 = β ενώ εμείς ξέρουμε ότι το β δεν είναι 0).
να μας δώσει μια σωστή ισότητα (θα προκύψει 0 = β ενώ εμείς ξέρουμε ότι το β δεν είναι 0). - αν
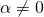 ,
,
η εξίσωση έχει ( μια ) λύσητην οποία μπορούμε να βρούμε εύκολαστο παράδειγμα που λύναμε είχαμε:
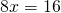 α=8 και β=16
α=8 και β=16
διαιρούμε λοιπόν με το 8 που είναι ο συντελεστής του χ
και παίρνουμε τη λύση
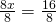 ή
ή 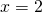
αρκεί να διαιρέσουμε με το συντελεστή του άγνωστου (το α) και η λύση θα είναι η
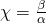 .
.
Όλη η παραπάνω διαδικασία εύρεσης της λύσης μιας εξίσωσης 1ου βαθμού φαίνεται στην εικόνα που ακολουθεί



οουυυφφφ Σας ευχαριστώ πολύ με ξεμπερδεύψατε!!!
Χαίρομαι ιδιαίτερα γι’ αυτό.
egw me ths e3iswseis den ta paw ka8olou kala giati den mporw na katalabo sthn teleutea pra3ei otan exoume
as poume 3 grammh klasmatos kai dipla 5 ti apotesma 8a kanw gia na to bro auto
–
Δήμητρα, αν κατάλαβα καλά ρωτάς τι σημαίνει το 3/5. Αυτό είναι το κλάσμα
και για να βρεις πόσο κάνει αρκεί να κάνεις τη διαίρεση 3:5=0,6. Αν έχεις φτάσει στο τέλος κι έχεις βρει x=3/5 το αφήνεις όπως είναι δεν είναι υποχρεωτικό το κλάσμα να το κάνεις δεκαδικό με την διαίρεση κι αυτό γιατί τις περισσότερες φορές η διαίρεση μπορεί να είναι ατελής. Αν με το 3/5 χρειαστεί να κάνεις πράξεις απλώς
θα κάνεις ομώνυμα στην περίπτωση που έχεις πρόσθεση ή αφαίρεση
(π.χ.
)
ή θα πολλαπλασιάσεις αριθμητή με αριθμητή και παρονομαστή με παρονομαστή στη περίπτωση που έχεις πολλαπλασιασμό
(π.χ.
)
αν δε έχεις διαίρεση αντιστρέφεις το δεύτερο κλάσμα και κάνεις πολλαπλασιασμό
(π.χ.
).
Επειδή οι εξισώσεις είναι ένα πολύ σημαντικό κομμάτι των μαθηματικών και θα σε «ταλαιπωρούν» μέχρι να τελειώσεις το σχολείο φρόντισε να «τα πας καλά μαζί τους» γι αυτό ασχολήσου λίγο παραπάνω με αυτές μέχρι να ξεπεράσεις τις δυσκολίες που έχεις. Σε πληροφορώ ότι είναι πολύ εύκολες, δες το σαν ένα παιχνίδι. Το κυριότερο μην αφήνεις απορίες άλυτες κι επειδή δεν είμαι σίγουρος ότι κατάλαβα καλά την απορία σου αν δεν σε βοήθησα μπορείς να αφήσεις ένα πιο αναλυτικό σχόλιο για να σου απαντήσω.
borei kapoios na mu e3igisei tn e3isosi auti : 2(x-1)+3(2-x)=4(x+2) aplos na mu tin e3igisei vima vima giati tin apadisi tn exo alla xoris e3igisei k perdeuomai…
Βιολέτα, απ’ ότι διάβασα στο άλλο σχόλιο που έχεις αφήσει, τώρα θα πας στην Α΄ Γυμνασίου. Η εξίσωση που έχεις, για να λυθεί θέλει μια διαδικασία που θα την μάθεις στην Β΄ Γυμνασίου και είναι αυτή που περιγράφεται στο παραπάνω άρθρο. Είναι λογικό να μπερδεύεσαι αφού τα περισσότερα από αυτά δεν τα έχεις διδαχθεί ακόμη. Κάνε λοιπόν υπομονή ένα χρόνο ακόμη :). Όσον αφορά την άλλη σου απορία για το ΕΚΠ θα σου απαντήσω σύντομα.
Δεν είμαι και πολυ σίγουρος ότι είμαι σωστός αλλα μόλις τελείωσα την β γυμνασιου και δεν είμαι άριστος αλλα μπορει να ειναι 2(χ-1) +3(2-χ)=4(+2)=2χ+2 +3χ+5χ=4χ+6χ=4χ+8χ=10χ,12χ=10χ 12χ/12=12/10 αδύνατη αλλα πιο πιθανό ειναι να έχω κάνει λάθος
egw exw tin aporia oti :
Mipos mporei se mia exisosi 1ou va8mou na uparxei apotelesma dekadiko??? giati merikes fores mou vgenei dekadikos … (ta leme stin ta3i )
Φυσικά και μπορεί να συμβαίνει αυτό, γιατί όχι; τι έχουν οι δεκαδικοί αριθμοί δεν είναι κι αυτοί αριθμοί; Εκτός κι αν λύνεις κάποιο πρόβλημα που δεν επιτρέπει σαν απάντηση δεκαδικό αριθμό, π.χ. σε κάποιο πρόβλημα ψάχνεις πόσα παιδιά έχει μια τάξη, δεν μπορείς να δεχτείς σαν λύση το 2,5. Επειδή όμως ξέρω γιατί ρωτάς στις ασκήσεις συνήθως το αποτέλεσμα το αφήνουμε σαν κλάσμα κι όχι σαν δεκαδικό. Και τα κλάσματα μια χαρά αριθμοί είναι και πολλές φορές «πιο σωστοί» από τους δεκαδικούς. Γιατί αν η διαίρεση είναι ατελής παράδειγμα: Έστω ότι λύνοντας την εξίσωση καταλήγεις
αν κάνεις την διαίρεση 1:3 και γράψεις
θα είναι λάθος γιατί αν αντικαταστήσεις το 0,3 στην εξίσωση δεν θα την επαληθεύει ενώ το 1/3 θα την επαληθεύει.
μηπως μπορειτε να με βοηθησετε να βρω ασκησεις για εξισωσεις 1ης Γυμνασιου????? που συνηθως βαζουν στα διαγωνισματα??????????????????????????????? περιμενω μηνυμα σας ως σημερααααααααα
Νεφέλη σου έχω στείλει μήνυμα.
μπορειτε να μου εξηγησετε πως κανουμε επιμεριστικη ιδιοτιτα
Γιώργο, η επιμεριστική ιδιότητα είναι η εξής:
αυτό πρακτικά σημαίνει ότι: όταν έχεις έναν αριθμό που πρέπει να πολλαπλασιαστεί με μια παρένθεση στην οποία μέσα υπάρχουν δύο ή και περισσότεροι αριθμοί τότε έχεις δύο επιλογές:
π.χ.
ή
π.χ.
Προφανώς βγαίνει και στις δύο περιπτώσεις το ίδιο αποτέλεσμα αυτή την έννοια έχει το “ = ” που υπάρχει στην ιδιότητα. Και προφανώς επίσης, διαλέγεις εσύ να χρησιμοποιήσεις όποιον από τους δύο τρόπους επιθυμείς.
Τώρα θα σκεφτείς κι εσύ αυτό που με ρωτάνε συνήθως οι μαθητές “γιατί χρειάζεται να ξέρω 2 τρόπους ο ένας δεν είναι αρκετός;” Η απάντηση είναι σίγουρα ΟΧΙ. Σκέψου για παράδειγμα πόσους δρόμους ξέρεις για να πας από το σπίτι σου στο σχολείο, μόνο έναν; προφανώς όχι έτσι αν μια μέρα ο δρόμος που ακολουθείς συνήθως είναι κλειστός (π.χ. γίνονται έργα) δεν γυρίζεις σπίτι αλλά επιλέγεις έναν από τους άλλους δρόμους που ξέρεις. Ακριβώς το ίδιο συμβαίνει κι εδώ, στον πρώτο τρόπο που αναφέραμε πιο πάνω είπαμε “κάνεις πρώτα τι πράξεις μέσα στην παρένθεση και μετά … “ τι γίνεται όμως όταν δεν έχεις τη δυνατότητα να κάνεις τις πράξεις μέσα στην παρένθεση; δεν την παρατάς αλλά ακολουθείς τον δεύτερο τρόπο.
Ας δούμε λοιπόν ένα παράδειγμα όπου συμβαίνει αυτό που προανέφερα. Έστω ότι έχεις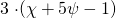 ,πράξεις μέσα στην παρένθεση δεν γίνονται, είναι γνωστό ότι πρόσθεση (κι αφαίρεση) γίνεται μόνο σε “ίδια αντικείμενα”. Έλα όμως που πρέπει να βγάλεις την παρένθεση για να προχωρήσεις. Εδώ λοιπόν χρησιμοποιείς τον δεύτερο τρόπο αφού η επιμεριστική ιδιότητα σου λέει “κάνε όποιον από τους δύο τρόπους θες ή μπορείς είναι και οι δύο το ίδιο”. Κάνουμε λοιπόν
,πράξεις μέσα στην παρένθεση δεν γίνονται, είναι γνωστό ότι πρόσθεση (κι αφαίρεση) γίνεται μόνο σε “ίδια αντικείμενα”. Έλα όμως που πρέπει να βγάλεις την παρένθεση για να προχωρήσεις. Εδώ λοιπόν χρησιμοποιείς τον δεύτερο τρόπο αφού η επιμεριστική ιδιότητα σου λέει “κάνε όποιον από τους δύο τρόπους θες ή μπορείς είναι και οι δύο το ίδιο”. Κάνουμε λοιπόν
και τέλος.
Επειδή το σχόλιό σου είναι κάτω από το άρθρο που αφορά στις εξισώσεις πρώτου βαθμού να σου τονίσω ότι εδώ στις εξισώσεις χρησιμοποιούμε συνεχώς την επιμεριστική ιδιότητα με αυτόν ακριβώς τον τρόπο κι ο λόγος είναι απλός “για να ελευθερώσουμε τον άγνωστο μέσα από τις παρενθέσεις”.
Πριν σου δείξω ένα παράδειγμα να σου υπενθυμίσω ότι αν έξω από την παρένθεση υπάρχει αρνητικός αριθμός αλλάζουμε πρόσημα όταν κάνουμε επιμεριστική π.χ.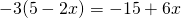 .
.
Αν έχεις υπομονή και διαβάζεις ακόμη κοίτα κι ένα παράδειγμα χρήσης της επιμεριστικής ιδιότητας στις εξισώσεις:
όπως βλέπεις εδώ δεν μπορούν να γίνουν πράξεις μέσα στις παρενθέσεις αφού μέσα σε αυτές υπάρχουν “ανόμοια” πράγματα αριθμοί και γράμματα. Σου θυμίζω και πάλι πρόσθεση γίνεται μόνο με ίδια πράγματα, προσθέτω αριθμούς με αριθμούς, χ με χ, ψ με ψ κτλ. Αναγκαζόμαστε λοιπόν να βγάλουμε τις παρενθέσεις να ελευθερωθούν όλα έτσι ώστε να πάρω τους αριθμούς από τη μια μεριά να τους προσθέσω και τα χ από την άλλη μεριά να τα προσθέσω. Για να δίωξω τις παρενθέσεις κάνω ΕΠΙΜΕΡΙΣΤΙΚΗ
δηλαδή x = 1.
Ότι σε κούρασα σε κούρασα είμαι σίγουρος γι αυτό ελπίζω όμως να σου έλυσα την απορία.
apo pia praxei proekipse to 28 sto 2o bima..
Από το 2 . 14 που είναι ακριβώς από πάνω του.
πως μπορω να λυσω αυτην την εξισωση 2χ-3(χ+5)=12
Σε αυτή την εξίσωση Εύα αφού δεν έχεις παρονομαστές θα ξεκινήσεις από το
2ο βήμα: Διώχνω παρενθέσεις με την βοήθεια της επιμεριστικής ιδιότητας
2χ – 3χ – 15 = 12, μετα για να μπορέσεις να τα συμμαζέψεις λίγο θα κάνεις το
3ο βήμα: Χωρίζω Γνωστούς από Άγνωστους
2χ – 3χ = 12 + 15, απ’ όπου προκύπτει
– χ = 3, κι αφού φτάσαμε ότι το μείον χ είναι ίσο με 3 τότε προφανώς το χ θα είναι ίσο με μείον 3, δηλαδή
χ = – 3
πωσ μπορω να λυσω την εξισωση (α-5)χ=4α+12 ωστε να ειναι αδυνατη?
Γιάννα,
όταν μια εξίσωση πρώτου βαθμού είναι:
αδύνατη καταλήγει στη μορφή 0χ=β, όπου β είναι οποιοσδήποτε αριθμός εκτός από το 0.
Ενώ όταν είναι αόριστη καταλήγει στη μορφή 0χ=0.
Λεπτομέρειες για το θέμα αυτό μπορείς να διαβάσεις κάνοντας κλικ εδώ.
Όσον αφορά τώρα στην άσκηση που έχεις, για να είτε αδύνατη είτε αόριστη απαραίτητη προϋπόθεση είναι να είναι 0 ο συντελεστής του χ. Επομένως θα πρέπει το α-5 να είναι ίσο με μηδέν.
Δηλαδή πρέπει α-5=0 ή αλλιώς α=5.
Για την τιμή αυτή του α που βρήκαμε θα τσεκάρουμε αν η εξίσωση βγαίνει αδύνατη ή αόριστη. Για να το πετύχουμε αυτό πηγαίνουμε στην εξίσωση και αντικαθιστούμε το α με τον αριθμό 5 και έχουμε:
(5-5)χ=4.5+12, δηλαδή 0χ=32 πράγμα που σημαίνει σύμφωνα με αυτά που είπαμε παραπάνω ότι η εξίσωση που έχουμε είναι αδύνατη όταν το α=5.
Παναγιώτη πάρα πολύ καλή προσπάθεια….βασικά τέλεια…..Τους βοηθάς όλους….Πολύ καλή επεξήγηση….Φοβερή ιστοσελίδα !!!!!! Συνέχισε να βοηθάς!!!!Χαιρετίσματα από ΣαΛοΝιΚάΡαααααααα!!
Gia sas 8elo na rotiso pos linete autei h exisosi μ(χ+6)-2=(2μ-1)χ+2 sas parakalo na dosete amesi apantisi giati einai polli simantiko
Αρχικά και αυτή η εξίσωση λύνεται όπως όλες οι εξισώσεις πρώτου βαθμού (η μεθοδολογία υπάρχει παραπάνω στο άρθρο)
Στο στάδιο αυτό τώρα θα πρέπει σύμφωνα με τη μεθοδολογία να διαιρέσουμε με τον συντελεστή του άγνωστου, δηλαδή με το μ – 2.
Αν όμως προσέξεις καλά τη μεθοδολογία (ρίξε μια ματιά στην εικόνα παραπάνω) θα δεις ότι κάνουμε διαίρεση με το συντελεστή του άγνωστου μόνο στην περίπτωση που αυτός δεν είναι ίσος με μηδέν.
Στην περίπτωσή μας όμως δεν το ξέρουμε αυτό αφού δεν γνωρίζουμε πόσο είναι το μ. Έτσι λοιπόν για να δώσουμε μια ολοκληρωμένη απάντηση θα διακρίνουμε δύο περιπτώσεις και θα πούμε ότι:
Άν δεχτούμε ότι το μ – 2 δεν είναι ίσο με μηδέν
, δηλαδή με άλλα λόγια αν το μ δεν είναι ίσο με 2, τότε το χ θα είναι
ενώ
Αν δεχτούμε ότι το μ – 2 είναι ίσο με το μηδέν,
δηλαδή αν δεχτούμε ότι το μ=2, τότε δεν μπορώ να διαιρέσω με το μ – 2 αλλά μπορώ να βάλω στην εξίσωση στη θέση του μ τον αριθμό 2 για να δω τι θα προκύψει. Έτσι λοιπόν θα έχουμε:
που για μ=2,
ή αλλιώς
πράγμα που είναι αδύνατο να συμβαίνει.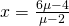
Καταλήγουμε λοιπόν στο ότι:
Αν το μ=2, η εξίσωση είναι αδύνατη
εν’ω αν το μ δεν είναι ίσο με 2 η εξίσωση έχει λύση την
Μπορεί κάποιος να μου εξηγήσει αυτες τις εξισώσεις? Δυσκολεύομαι ιδιαίτερα
α) χ-2χ-1=3(χ+1)
3 4
β)4-5χ-3(χ-1)=2χ-6
12 2
Πάω Β’ γυμν. αλλά στις εξισώσεις χρειάζομαι ΒΟΗΘΕΙΑ παρακαλώ πως τις λύνω?…
α)
πρώτα βγάζεις τις παρενθέσεις κάνοντας επιμεριστική ιδιότητα
έπειτα χωρίζεις γνωστούς άγνωστους
στη συνέχεια κάνεις πράξεις
και τέλος διααιρείς με τον συντελεστή του άγνωστου
έτσι προκύπτει
β) Όμοια
Gia sas 8elo na rotiso pos linete autei h exisosi meta apo to 2 bima 2(x-1)-3(x+1)<4(x+2)+12 sas parakalo na dosete amesi apantisi,einai polli simantiko
Σοφία συγνώμη για την καθυστερημένη απάντηση αλλά ήμουν διακοπές σε μέρος που δεν είχα σύνδεση στο διαδίκτυο.
Η ανίσωση που μου δίνεις λύνεται ως εξής:
Πρώτα με επιμεριστική ιδιότητα διώχνουμε τις παρενθέσεις
Μετά χωρίζουμε τους γνωστούς από τους άγνωστους όρους (όποιος όρος αλλάζει μέλος πρέπει να αλλάξει και πρόσημο)
Κάνουμε πράξεις σε κάθε μέλος ξεχωριστά
Διαιρούμε με το -5 που είναι ο συντελεστής του άγνωστου κι επειδή είναι αρνητικός αριθμός αλλάζει φορά η ανισότητα
Gia sas uelo na moy lisete mia exisosi poy na exei kai paranomastes kai parenuesis sas parakalo:)
Εδώ αποφασίζες τι θέλεις να διώξει πρώτο τους παρονομαστές ή τις παρενθέσεις;
Εγώ θα δίωξω τις παρενθέσεις κάνοντας χρήση της επιμεριστικής ιδιότητας:
Τώρα πολλ/ζουμε με το 6 που είναι το ΕΚΠ των παρονομαστών
Απλοποιούμε τους παρονομαστές (προσοχή ξαναμπαίνουν παρενθέσεις)
Διώχνουμε και τις παρενθέσεις
χωρίζουμε γνωστούς – άγνωστους
κάνουμε πράξεις και στα δύο μέλη
και τέλος διαρούμαι με το -18 που είναι ο συντελεστής του άγνωστου
άρα x=0
stop proto vhma stin triti grami to 3x+2.14 pos proekipse?
Δημήτρη, στο στάδιο που πολλαπλασιάζουμε με το ΕΚΠ έχουμε στόχο να διώξουμε τους παρονομαστές. Έτσι λοιπόν κάνουμε απλοποιήσεις, δηλαδή διαιρούμε το ΕΚΠ με τον παρονομαστή. Στο σημείο που αναφέρεσαι αν προσέξεις θα δεις ότι έχουμε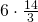 κάνουμε λοιπόν τη διαίρεση 6:3 που μας κάνει 2 κι έτσι μένει το
κάνουμε λοιπόν τη διαίρεση 6:3 που μας κάνει 2 κι έτσι μένει το 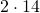
eimai 2ra gimnasiou kai apo e3iswseis dn 3erw XRISTO.. mpwreis ligo na grapseis mia pra3i na m e3igisis pws linete?? euxaristo!
Τις εξισώσεις θα τις μάθεις τώρα στη Β Γυμνασίου δικαιολογημένα να μην μπορεις τώρα να λύσεις εξισώσεις. Κάνε λίγο υπομονή.
deen katalabeno tpt pos mporo na to antimetopiso?
Αν δεν καταλαβαίνεις το πιο πιθανό είναι να έχεις κενά από προηγούμενα μαθήματα. Οι εξισώσεις είναι ομολογουμένως ένα δύσκολο κομμάτι. Αν έχεις και κενά προφανώς γίνεται ακόμη δυσκολότερο. Επειδή όμως είναι πάρα πολύ σημαντικό για να μπορέσεις να συνεχίσεις με τα μαθηματικά να έχεις μάθει καλά τις εξισώσεις θα πρέπει να το παλέψεις. Εγώ σου προτείνω να ξεκινήσεις το διάβασμα από προηγούμενες ενότητες. Ξεκινόντας από εκεί που καταλαβαίνεις και προχωρόντας παρακάτω σιγά σιγά. Για να μπορέσεις να λύσεις εξισώσεις θα πρέπει τουλάχιστον να ξέρεις:
Πράξεις με θετικούς και αρνητικούς, να μετατρέπεις κλάσματα σε ομώνυμα με τη βοήθεια του ΕΚΠ κ.α. Ρίξε μια ματιά και στα παρακάτω άρθρα:
Θέλω να μάθω…τι είναι η εξίσωση
Θέλω να μάθω … πότε μια εξίσωση λέγεται αδύνατη και πότε αόριστη
Θέλω να μάθω…πως διώχνω τους παρονομαστές από μια εξίσωση
Δες και αυτό το βίντεο
πως μπορω να λυσω αυτες τις τρεις εξισωσεις 1)3-χ=2χ+7χ 2)-2χ-5=6χ-4 3)χ-5+2χ-4=10χ
Δημήτρη, αφού διαβάσεις καλά το άρθρο παραπάνω και προσπαθήσεις λίγο περισσότερο πιστεύω ότι θα καταφέρεις να λύσεις αυτές τις εξισώσεις που κατα τη γνώμη μου είναι εύκολες. Εγώ θα λύσω τη μια από αυτές και θα σε αφήσω να λύσεις με τον ίδιο τρόπο τις υπόλοιπες. Αν δεν τα καταφέρεις μου το λες. Πάμε λοιπόν:
Το πρώτο πράγμα που κάνουμε σε μια εξίσωση είναι να διώξουμε τους παρονομαστές για να δουλεύουμε πιο άνετα, ευτυχώς αυτή η εξίσωση δεν έχει παρονομαστές.
Μετά διώχνουμε τις παρενθέσεις ώστε να μπορούμε να κάνουμε πράξεις, ευτυχώς εδώ ούτε παρενθέσεις έχουμε. (Γι’ αυτό σου είπα και παραπάνω ότι είναι εύκολες αφού η μισή δουλειά έχει γίνει). Αφου λοιπόν τελειώσαμε με τα δύο πρώτα βήματα προχωράμε στο επόμενο που είναι να χωρίσω τους γνωστούς από τους άγνωστους όρους για να μπορέσω να συμμαζέψω λίγο την εξίσωση. Στο βήμα αυτό προσπαθούμε στο ένα μέλος να έχουμε όλους τους όρους που έχουν το χ και στο άλλο τους καθαρούς αριθμούς, προσοχή όμως γιατί όταν παίρνεις έναν όρο από τη μια μεριά και τον πηγαίνεις στην άλλη πρέπει να του αλλάζεις το πρόσημο. Επομένως η εξίσωσή μας τώρα θα γίνει:
Tο μόνο που μας έμεινε τώρα είναι να διαιρέσουμε και από τις δύο μεριές με τον συντελεστή του άγνωστου (τον αριθμό που βρίσκεται μπροστά από το χ). Οπότε έχουμε
Αυτό ήταν όλο, σειρά σου τώρα
Συγχαρητηρια ειμαι 38 χρ κανω ανοικτο πανεπισημιο και σε 5 λεπτα με εσας εμαθα οτι δεν μπορεσα να καταλαβω στο σχολειο. και παλι μπραβο σας
4x-1 4 9x+1
——– = – —– ( -1 – ——– )
6 3 18
Μπορείται να με βοηθήσετε σας παρακαλώ, εχουν σπάσει τα νεύρα μου
Νικολέτα, γράψε την εξίσωση σε ένα χαρτί, βγάλτη φωτογραφία με το κινητό και στείλτη στο email μου. ή προσπάθησε να τη γράψεις πιο καλά διαβάζοντας εδώ:http://mathland.gr/archives/5115 ή προσπάθησε από εδώ γιατί δεν βγάζω άκρη.
Σας την ξανά έστειλα ελπίζω τωρα να μπορειται να καταλάβετε τι εννοώ
Νικολέτα, πολύ καλή η προσπάθειά σου μπράβο σου. Θα προσπαθήσω να σε βοηθήσω να δεις πως λύνονται αυτές οι εξισώσεις μόνο που θα κάνω κάτι διορθώσεις στην εξίσωση γιατί συγκρίνοντας τα δύο μηνύματα που έχεις στείλει υποθέτω ότι η εξίσωση πρέπει να είναι αυτή:
αν δεν είναι αυτή θα μου την διορθώσεις.
Λύση:
Πρώτα απ’ όλα θα βγάλουμε την παρένθεση:
μετά πρέπει να διώξουμε τους παρονομαστές. Αυτό θα το πετύχουμε αν πολλαπλασιάσουμε κάθε όρο με το ΕΚΠ των παρονομαστών που εδώ είναι το 6 το 3 και το 18. ΕΚΠ(3,6,18)=18, οπότε πολλαπλασιάζουμε τα πάντα με το 18 κι έχουμε:
μετά από τις απλοποιήσεις σου μένουν:
βγάζουμε τώρα τις παρενθέσεις κάνοντας επιμεριστική ιδιότητα:
Χωρίζουμε τώρα γνωστούς από άγνωστους: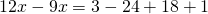 ή
ή 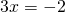 και τελειώνουμε διαρώντας με το συντελεστή του άγνωστου:
και τελειώνουμε διαρώντας με το συντελεστή του άγνωστου:
τελικά: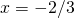
Στην εξίσωση που διορθώσατε δεν υπάρχει το μείον μπροστά απο την παρένθεση ολα τα αλλα ειναι σωστά.
Θα σας ηταν εύκολο να μου δώσετε το εμαιλ σας για να σας στειλω εκεί άλλη μια άσκηση που εχω; Γιατι απο εδώ σίγουρα θα κανω παλι κατι λάθος. Πάντως σας ευχαριστώ παρα πολυ
σου έστειλα email
mporeite na mou peite ena site pou vazoun tis askiseis gia ta diagonismata kai na exei tis luseis?
Θεοδόση πες μου λίγο πιο συγκεκριμένα για ποια τάξη θέλεις και για ποια διαγωνίσματα εννοείς;
πως λυνεται η εξισωση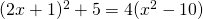 ???
???
Φωτεινή πρέπει να ξέρω τι τάξη πας για να δούμε την άσκηση σύμφωνα με αυτά που έχεις διδαχθεί
γ γυμνασιου !!
Πρώτα πρέπει να διώξουμε τις παρενθέσεις:
Για το λόγο αυτό στο α΄ μέλος αναπτύσουμε την ταυτότητα και στο β΄ μέλος κάνουμε επιμεριστική:
Τα μαζεύουμε όλα στο α΄ μέλος και κάνουμε πράξεις (αναγωγή όμοιων όρων):
Η εξίσωση που προέκυψε είναι πρώτου βαθμού, άρα χωρίζω γνωστούς από άγνωστους:
και στη συνέχεια διαιρούμε με τον συντελεστή του άγνωστου
Παναγιώτη συγχαρητηρια για την δουλεια που κανεις.Είμαι στο μεταπτυχιακό τμημα του ΠΑΜΑΚ (UOM) και φυσικα σαν 3οδεσμιτισσα ( δεν λεω ηλικια) δεν είχα καθολου καλη σχεση με τα μαθηματικα .Η σελιδα σου με βοηθαει παρα πολυ. θα σε παρακολουθώ Εχω και αλγεβρικεσ μορφεσ συναρτησεων και διαγραμματα, μπορεισ να με βοηθησεις?
Ευαγγελία, σ’ ευχαριστώ για τα καλά σου λόγια. Αν έχεις απορίες στείλε μήνυμα ή άφησε σχόλιο κι αν μπορώ θα βοηθήσω.
ΓΕΙΑ ΣΑΣ! ΠΑΩ 2α ΓΥΜΝΑΣΙΟΥ ΚΑΙ ΕΝΩ ΕΧΩ ΚΑΑΛΑΒΕΙ ΤΟΥΣ ΤΥΠΟΥΣ ΕΞΙΣΩΣΕΩΝ ΚΑΙ ΑΝΙΣΩΣΕΩΝ ΔΕΝ ΜΠΟΡΩ ΜΕ ΤΙΠΟΤΑ ΝΑ ΤΟΥΣ ΕΦΑΡΜΟΣΩ (ΑΝ ΚΑΙ ΟΙ ΑΣΚΗΣΕΙΣ ΤΗΣ ΚΑΘΗΓΗΤΡΙΑΣ ΔΕΝ ΕΙΝΑΙ ΚΑΙ ΟΙ ΠΙΟ ΕΥΚΟΛΕΣ) ΚΑΙ ΟΙ ΕΞΕΤΑΣΕΙΣ ΠΛΗΣΙΑΖΟΥΝ! ΤΙ ΝΑ ΚΑΝΩ;
Για μια σύντομη επανάληψη για τις εξετάσεις σου προτείνω να διαβάσεις αυτό
Επανάληψη Β΄Γυμνασίου
Για τις εξισώσεις και τις ανισώσεις ρίξε μια ματιά και σε αυτά:
Βίντεο 1
Βίντεο 2
Βίντεο 3
Βίντεο 4
Βίντεο 5
Και ότι απορίες έχεις να μου στείλεις μήνυμα με τη συγκεκριμένη άσκηση και το που ακριβως μπερδεύεσαι μήπως και μπορώ να σε βοηθήσω
mporeite na lisete mia eksisiosi 2ou vathmou gia 3h gumn
Παναγιώτη, μπορείς να βρεις εδώ:Εξίσωση 2ου βαθμού, Λυμένα παραδείγματα κι εδώ: Βιντεομαθήματα Γ΄ Γυμνασίου
Γεια σας! Ειμαι μαθητρια Α’ Λυκειου και δυσκολευομαι παρα πολυ με την Αλγεβρα συγκεκριμενα εξισωσεις , ανισωσεις και τα (S,P) ! παλι καλα βρηκα εσας και μου λυσατε τις αποριες σχετικα με τις ανισωσεις και εξισωσεις! Γινετε να κανουμε κατι και για τα S,P? δεν με βολευει καθολου η διατυπωση του βιβλιου (αλλα ουτε και τις καθηγητριας μου) περιμενω νεα σας! Την Δευτερα γραφω αλγεβρα οποτε … δωστε και σωστε :Ρ
Παρακαλω πολυ βοηθειστε με βημα-βημα στο τελευταιο μερος της συναρτησης.
Για να βρουμε το μεγιστο ΤR (συνολικο εσοδο) βρισκουμε πρωτα την ποσοτητα που μεγιστοποιει την συναρτηση
τουTR.
TR=PQ=(2-0,01)Q=2Q-0,008Qεις τη 2 το Q(μονο).
dTR/dQ=0=>2-0,016Q=0=>0,016Q=2=>Q=2/0,016=>Q=125 και
d εις την 2TR/dQ εις την 2(μονο το Q)<0 dεις την2TR/dQ εις την 2,μονο τοQ=-0,016.
Επειδη δεν ειμαι δεινος χρηστης του Η/Υ πιστευω να καταλαβαινετε τι θελω.Με ενδιαφερει μονο το τελευταιο σκελος
με τις παραγωγους και πως λυνεται.
2.(-χ+3)+3.χ/5=-(χ-1)/3+4.-χ+5/10 πως λυνεται αυτη η εξισωση μορειτε να με βοηθησετε?
γεια σας θελω να πειτε τον τροπο αναγωγη ομιιν ωρον αγνωστον και γωοστον των αριθμων
3χ+χ+3χ+4χ=-2+36+20
3χ+χ+3χ+4χ=-2+36+20
11χ=54
γεια σας θα ηθελα να μαθω γιατι σε μια εξισωση πρωτου βαθμου οταν αλλαζει ενα ψηφιο μερος αλλαζει και προσημο? σας παρακαλω απαντηστε μου αυριο γραφω διαγωνισμα και αυτο θα πεσει
Δανάη, θα προσπαθήσω να στο εξηγήσω με ένα απλό παράδειγμα.
Ας υποθέσουμε ότι έχουμε να λύσουμε την εξίσωση:
για να καταφέρουμε να βρούμε τη λύση πρέπει να απομονώσουμε τον άγνωστο x στο ένα μέλος. Για να το πετύχουμε αυτό πρέπει να εξαφανίσουμε από δίπλα του τον αριθμό +3. Για να εξουδετερώσουμε το +3 προσθέτουμε και στα δύο μέλη τον αντίθετό του, δηλαδή τον -3. Έτσι έχουμε λοιπόν:
Επιδή +3-3=0 προκύπτει:
Φαίνεται λοιπόν ότι το +3 μετακινήθηκε στο δεύτερο μέλος και έχει αλλάξει πρόσημο. Στην πραγματικότητα όμως δεν συναίβει αυτό. Αυτό που στην πραγματικότητα κάναμε είναι να εξουδετερώσουμε το +3 από το πρώτο μέλος προσθέτοντας και στα δύο μέλη το -3. Για λόγους συντομίας παραλήπουμε να γράφουμε αυτό το βήμα και γι’ αυτό φαίνεται σαν να έχουμε μετακινήσει το +3 από το πρώτο στο δεύτερο μέλος (και φαίνεται να άλλαξε πρόσημο).
γεια σας όταν έχω αυτή την εξίσωση πως μπορώ να τη λύσω ;
Πρώτα θα διώξουμε τις παρενθέσεις κάνοντας επιμεριστική:
Προσοχή έχω κάνει κάποιες απλοποιήσεις, όπως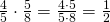 και
και 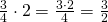
Στη συνέχεια για να διώξουμε τους παρονομαστές πολλαπλασιάζουμε όλους τους όρους με το ΕΚΠ=80
Μετά από τις απλοποιήσεις και τη διαγρφή των παρονομαστών μένει:
Καλησπερα! Θελω να με βοηθησετε σε αυτην την εξισωση : 3(χ-2)+(χ-1)=-(1-2χ)
Ιωάννα,
πρώτα διώχνεις τις παρενθέσεις κάνοντας επιμεριστική ιδιότητα:
στη συνέχεια χωρίζεις τους γνωστούς από τους άγνωστους:
μετά κάνεις πράξεις:
και τέλος διαιρείς με το συντελεστή του x,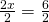 άρα
άρα 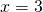
να σας ρωτησω κατι εε πως βαζουμε τα πρωσημα μπροσατα δλδ οταν εχουμε πολλαπλασιασμο – με – μας κανει + αλλα οταν εχουμε προσθεσηη? και το + με + και το + με – …αυτα δεν τα ξερω καθολου μπορειτε να με βοηθησετεεεε?
Σάρα,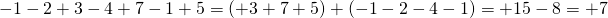
για την πρόσθεση πρέπει να ξέρεις τα παρακάτω:
1. Αν θέλεις να βρεις το άθροισμα θετικών αριθμών, τους προσθέτεις (χωρίς να λαμβάνεις υπόψη σου το πρόσημο) και στο αποτέλεσμα βάζεις το πρόσημο +.
π.χ. +1+2+3+4=+10
2. Αν θέλεις να βρεις το άθροισμα αρνητικών αριθμών, τους προσθέτεις (χωρίς να λαμβάνεις υπόψη σου το πρόσημο) και στο αποτέλεσμα βάζεις το πρόσημο -.
π.χ. -1-2-3-4=-10
3. Αν θέλεις να βρεις το άθροισμα ενός θετικού και ενός αρνητικού, τους αφαιρείς(χωρίς να λαμβάνεις υπόψη σου το πρόσημο από τον μεγαλύτερο αφαιρείς τον μικρότερο) και στο αποτέλεσμα βάζεις το πρόσημο του «ισχυρότερου» δηλαδή αυτού που χωρίς πρόσημο είναι μεγαλύτερος.
π.χ. -3+7=+4 (γιατί 7 μεγαλύτερο του 3 και το 7 έχει πρόσημο +) ενώ -9+5=-4 (γιατί το 9 είναι μεγαλύτερο από το 5 και το 9 έχει πρόσημο -)
4. Αν έχεις πολλούς θετικούς και πολλούς αρνητικούς, τότε προσθέτεις όλους τους θετικούς και βρίσκεις έναν θετικό, προσθέτεις όλους τους αρνητικούς και βρίσκεις έναν αρνητικό και τέλος αφαιρείς αυτά τα δύο νούμερα βάζοντας το πρόσημο του «ισχυρότερου».
π.χ.
Αν θες μπορείς να κάνεις εξάσκηση εδώ: Πρόσθεση – Αφαίρεση
Καλησπέρα.Έχω απορία σε μια εξίσωση όσον αφορά την επίλυση της ,η εξίσωση είναι αυτή: χ3(τρίτης) -125=0!
Έχω άλλη μια απορία ,με την λύση μιας εξίσωσης ,την είδα λυμένη αλλά δεν κατάλαβα από που προκύπτει το αποτέλεσμα που είναι -2!Η εξίσωση: χ4(τετάρτης)+8χ =0 γίνετε χ(χ3(τρίτης)+8)=0
χ=0 ή χ3(τρίτης)=-8
χ=0 ή χ=-(ρίζα του 8 υψωμένη στην τρίτη)=-2
Νίκη,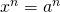 δηλαδή να έχεις απομονωμένο τον άγνωστο στο πρώτο μέλος και απομονωμένο τον αριθμό στο δεύτερο μέλος. Φροντίζεις δε τον αριθμό να τον γράψεις υπό μορφή δύναμης με τον ίδιο εκθέτη που έχει και ο άγνωστος. Στη συνέχεια αν ο εκθέτης είναι μονός αριθμός προκύπτει σαν λύση x=a ενώ αν ο εκθέτης είναι ζυγός (και το a θετικό) προκύπτουν δύο λύσεις: x=a ή x=-a (αν το a είναι αρνητικό είναι αδύνατη)
δηλαδή να έχεις απομονωμένο τον άγνωστο στο πρώτο μέλος και απομονωμένο τον αριθμό στο δεύτερο μέλος. Φροντίζεις δε τον αριθμό να τον γράψεις υπό μορφή δύναμης με τον ίδιο εκθέτη που έχει και ο άγνωστος. Στη συνέχεια αν ο εκθέτης είναι μονός αριθμός προκύπτει σαν λύση x=a ενώ αν ο εκθέτης είναι ζυγός (και το a θετικό) προκύπτουν δύο λύσεις: x=a ή x=-a (αν το a είναι αρνητικό είναι αδύνατη)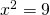 είναι απομονωμένα το χ και το 9 το καθένα στο δικό του μέλος. Επειδή το χ είναι υψωμένο στη δευτέρα προσπαθείς να γράψεις το 9 σαν δύναμη με εκθέτη το 2, αυτό είναι εύκολο γιατί
είναι απομονωμένα το χ και το 9 το καθένα στο δικό του μέλος. Επειδή το χ είναι υψωμένο στη δευτέρα προσπαθείς να γράψεις το 9 σαν δύναμη με εκθέτη το 2, αυτό είναι εύκολο γιατί 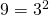 . Οποτε η εξίσωση γίνεται
. Οποτε η εξίσωση γίνεται 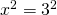 . Τώρα επειδή ο εκθέτης είναι ζυγός έχουμε δύο λύσεις χ=2 ή χ=-2
. Τώρα επειδή ο εκθέτης είναι ζυγός έχουμε δύο λύσεις χ=2 ή χ=-2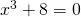 , πρώτα απομονώνουμε
, πρώτα απομονώνουμε 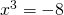 μετά γράφουμε το 8 σαν δύναμη με εκθέτη το 3 με λίγες δοκιμές βρίσκεις ότι
μετά γράφουμε το 8 σαν δύναμη με εκθέτη το 3 με λίγες δοκιμές βρίσκεις ότι 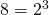 . Έτσι η εξίσωση γίνεται
. Έτσι η εξίσωση γίνεται 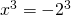 , άρα έχουμε μια λύση την χ=-2 (μία λύση γιατί ο εκθέτης είναι μονός).
, άρα έχουμε μια λύση την χ=-2 (μία λύση γιατί ο εκθέτης είναι μονός).
για να λύσεις τέτοιες εξισώσεις προσπαθείς να φέρεις την εξίσωση στη μορφή:
Παράδειγματα:
1.
2.
3. Ας δούμε τώρα την άσκηση στην οποία έχεις απορία:
απομονώνουμε:
κάνουμε το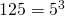 :
:
άρα χ=5
Που μπορω να βρω εξισωσεις β γυμνασιου σας παρακαλω αν μπορειται απαντηστε μου
Κατέβασε από αυτό το λινκ: https://onedrive.live.com/redir?resid=508331B44FC46ABA%2111558
ευχαριστω πολυ
a) (+7)+(-8)+(-2)=
b) (-5)+(-9)+(+6)=
g) (+2)+(-11)+(+3)=
d) (-3)+(-12)+(-17)=
e) (+4)+(-5)+(+9)+(-16)=
st) (-11)+(+7)+(-29)+(+13)=
z) (+14)+(-8)+(10)+(+7)=
Μαρία,
πιστεύω πως ο καλύτερος τρόπος να δουλεύεις σε αυτές τις περιπτώσεις είναι ο εξής:
1ον) προσθέτεις όλους τους θετικούς και στο αποτέλεσμα βάζεις πρόσημο +
2ον) προσθέτεις όλους τους αρνητικούς και στο αποτέλεσμα βάζεις πρόσημο –
3ον) αφαιρείς τον θετικό με τον αρνητικό και στο αποτέλεσμα βάζεις το πρόσημο του μεγαλύτερου αριθμού από τους δύο βλέποντας τους όμως χωρίς πρόσημο.
Δηλαδή:
a) (+7)+(-8)+(-2)= +7 -10 = -3
b) (-5)+(-9)+(+6)= +6 -14 = -8
g) (+2)+(-11)+(+3)= +5 -11 = -6
d) (-3)+(-12)+(-17)= -32
e) (+4)+(-5)+(+9)+(-16)= +13 -21 = -8
st) (-11)+(+7)+(-29)+(+13)=
z) (+14)+(-8)+(10)+(+7)=
2˙Χ-(2.36-1.15)=1.05 πως μπορώ να το λύσω για να το καταλάβω; Ευχαριστώ
Πρώτα απ’ όλα πρέπει να βγάλεις τις παρενθέσεις με προσοχή γιατί υπάρχει – έξω από την παρένθεση και πρέπει να αλλάξουν τα πρόσημα:
στη συνέχεια χωρίζεις τους γνωστούς όρους από τους άγνωστους και πάλι με προσοχή γιατί όποιος όρος αλλάζει μέλος αλλάζει και πρόσημο:
τώρα κάνεις τις πράξεις:
και τέλος διαιρείς με το συντελεστή του x
οπότε καταλήγεις χ=1,13
Θελω να λυισω την εξισωση 4×-3 γραμμη κλασματος 2 – × γραμμη κλασματος 3 = 5 γραμμη κλασματος 6 βοηθηστεεε
Αντζελίνα,
η εξίσωση που μου δίνεις πρέπει να ξέρω ακριβώς τι μορφή έχει και ακόμη να γνωρίζω σε ποια τάξη είσαι. Θα κάνω μια προσπάθεια υποθέτοντας ότι η εξίσωσή σου είναι αυτή:
Σε τέτοιου είδους εξισώσεις όπου έχεις ένα κλάσμα ίσο με ένα άλλο κλάσμα συνήθως κάνουμε «χιαστί» για να απαλλαγούμε από τους παρονομαστές, δηλαδή:
κάνοντας πάλι «χιαστί»
τώρα χωρίζουμε τους γνωστούς από τους άγνωστους όρους:
Γεια σας,
Έχω μια πολύ σύντομη απορία σε μια εξίσωση η οποία έχω μπερδευτεί για το τι πρόσημο θα βάλω.
Η εξίσωση είναι:
6 ( χ – 1 ) – ( 3 χ + 11 ) = – (3 χ + 8)
Πάει: 6χ – 6 ….
και μετά τι πρόσημο πάει για το 3χ, πλην όπως είναι έξω από την παρένθεση, ή σήν, για να δείξει ότι τα ενώνει – επειδή απλά δεν είναι μέσα στην παρένθεση; Έχω μπερδευτεί.
Δεν χρειάζομαι την λύση της εξίσωσης, μόνο το τι πρόσημο πάει σε τέτοιου είδους καταστάσεις και θα σας παρακαλούσα πολύ να μου το γράψετε όσο πιο σύντομα μπορείτε διότι αύριο έχω εξετάσεις. Ευχαριστώ πολυ!!!
++Επίσης πάω Β’ Γυμνασίου.
Βασιλική, ό,τι βλέπεις μέσα στην παρένθεση έχει πρόσημο: στην πρώτη παρένθεση είναι +χ -1, στην δεύτερη είναι +3χ +11 και στην τρίτη είναι +3χ +8. Όταν βγάζεις τις παρενθέσεις,
αν μπροστά υπάρχει + τότε δεν αλλάζουμε πρόσημα ενώ αν μπροστά από την παρένθεση υπάρχει – αλλάζουν πρόσημο τα περιεχόμενα της παρένθεσης.Έτσι έχουμε:
Η πρώτη παρένθεση έχει μπροστά της +6 ,άρα δεν αλλάζω πρόσημα: 6(χ-1)=6χ-6
Η δεύτερη παρένθεση έχει μπροστά της -, άρα αλλάζω πρόσημο στα περιεχόμενα: -(3χ+11)=-3χ-11 και τέλος
στην τρίτη παρένθεση έχω πάλι – έξω, άρα αλλάζω: -(3χ+8)=-3χ-8
ΤΕΛΙΚΑ 6(χ-1)-(3χ+11)=-(3χ+8) γίνεται: 6χ-6-3χ-11=-3χ-8