Σε προηγούμενο άρθρο είδαμε πως μπορούμε να βρούμε την εξίσωση μιας ευθείας. Είχαμε αναφέρει λοιπόν ότι πρέπει να μας έχουν δοθεί οπωσδήποτε ο συντελεστής διεύθυνσης (λ) κι ένα σημείο Α(χΑ,ψΑ) της ευθείας. Μάλιστα είχαμε λύσει κι ένα παράδειγμα όπου και τα δύο (συντελεστής και σημείο) δίνονταν άμεσα. Σήμερα θα δούμε με ποιους τρόπους θα μπορούσαν να μας δώσουν (έμμεσα) το συντελεστή διεύθυνσης.
- Μέσω της γωνίας που σχηματίζει η ευθεία με τον άξονα χ΄χ:
Αν η ευθεία (ε) η οποία ζητάμε σχηματίζει γωνία ω με τον άξονα χ΄χ, τότε ισχύει: λε=εφω - Μέσω δύο σημείων Α και Β από τα οποία διέρχεται η ευθεία:
Έστω ότι η ευθεία (ε) που θέλουμε να βρούμε διέρχεται από τα σημεία Α(xA,yΑ) και Β(xΒ,yΒ), τότε για το συντελεστή διεύθυνσης λε της ευθείας (ε) ισχύει:
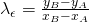(μόνο για το Λύκειο) - Μέσω της παραλληλίας της ζητούμενης ευθείας με μια άλλη ευθεία που μας έχουν δώσει:
Αν η ευθεία (ε) που ψάχνουμε είναι παράλληλη με μια ευθεία (δ) μας έχουν δώσει, τότε ισχύει: λε = λδ. - Μέσω της καθετότητας της ζητούμενης ευθείας με άλλη ευθεία που μας έχει δοθεί:
Αν η ζητούμενη ευθεία (ε) είναι κάθετη σε δοσμένη ευθεία (δ), τότε ισχύει: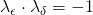
- Μέσω της παραλληλίας της ζητούμενης ευθείας με ένα διάνυσμα που μας έχουν δώσει (Β΄ Λυκείου Κατεύθυνση):
Αν η ευθεία που αναζητάμε είναι παράλληλη με ένα διάνυσμα που μας έχουν δώσει με συντελεστή λδ, τότε ισχύει: λε = λδ. - Μέσω της καθετότητας της ζητούμενης ευθείας με ένα διάνυσμα που μας έχει δοθεί (Β΄ Λυκείου κατεύθυνση):
Αν η ευθεία μας είναι κάθετη σε κάποιο διάνυσμα που έχει συντελεστή διεύθυνσης λδ, τότε θα ισχύει:.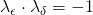
Συγκεντρώνοντας όλα τα παραπάνω σε ένα πίνακα έχουμε:
| Eυθεία (ε) με… | Υπολογισμός του λε |
|---|---|
| (ε) και χ΄χ να σχηματίζουν γωνία ω | λε = εφω |
| (ε) να διέρχεται από Α(xA,yA) και Β(xB,YB) |  |
| (ε) παράλληλη προς την ευθεία (δ) | λε = λδ |
| (ε) κάθετη με την ευθεία (δ) |  |
| (ε) παράλληλη με το διάνυσμα | λε = λδ |
| (ε) κάθετη με το διάνυσμα | |
Και για να ολοκληρώσουμε αυτά που είχαμε πει για τον προσδιορισμό της εξίσωσης μιας ευθείας θα τελειώσουμε βλέποντας με ποιο άλλο τρόπο θα μπορούσαν να μας δώσουν ένα σημείο από το οποίο περνά η ευθεία. Αν λοιπόν δεν δοθεί άμεσα θα μπορούσε να δοθεί ως τομή δύο άλλων ευθειών. Στην περίπτωση αυτή για να βρούμε τις συντεταγμένες του σημείου που χρειαζόμαστε πρέπει να λύσουμε το σύστημα αυτών των δύο εξισώσεων (αυτό θα μπορούσε να γίνει μόνο για τις Γ΄ Γυμνασίου, Α΄ Λυκείου και στην Κατεύθυνση της Β΄ Λυκείου. Στη Β΄ Γυμνασίου το σημείο θα δίνεται άμεσα.
Επειδή το άρθρο είναι σχετικά μεγάλο τα απαραίτητα παραδείγματα θα τα λύσουμε στο επόμενο.
Kurie na sas rwtisw kati ???(gt twra pou exoume katalipsi dn eixa tin eukeria) mporei na arxizei i grammi apo to 0 kai na pigenei pros ta katw k na 3anaanevenei ???(8a sas dei3w pws enow stin ta3i )!!!!
Αν κατάλαβα καλά τι εννοείς η απάντηση είναι ναί μπορεί. Ρίξε και μια ματιά στην εικόνα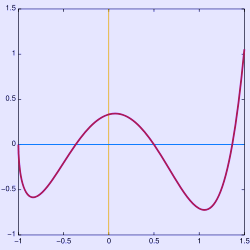
καλησπέρα. δεν ισχύει επίσης ο τύπος -Α/Β όπως δείχνει το κεφάλαιο 2.2 του βιβλίο προσανατολισμου β λυκείου;
Ναι ισχύει ο τύπος αυτός (λ=-Α/Β) αλλά μόνο στη περίπτωση που η ευθεία έχει τη μορφή Αχ+Βψ+Γ=0 και όχι για τη μορφή ψ=αχ+β.