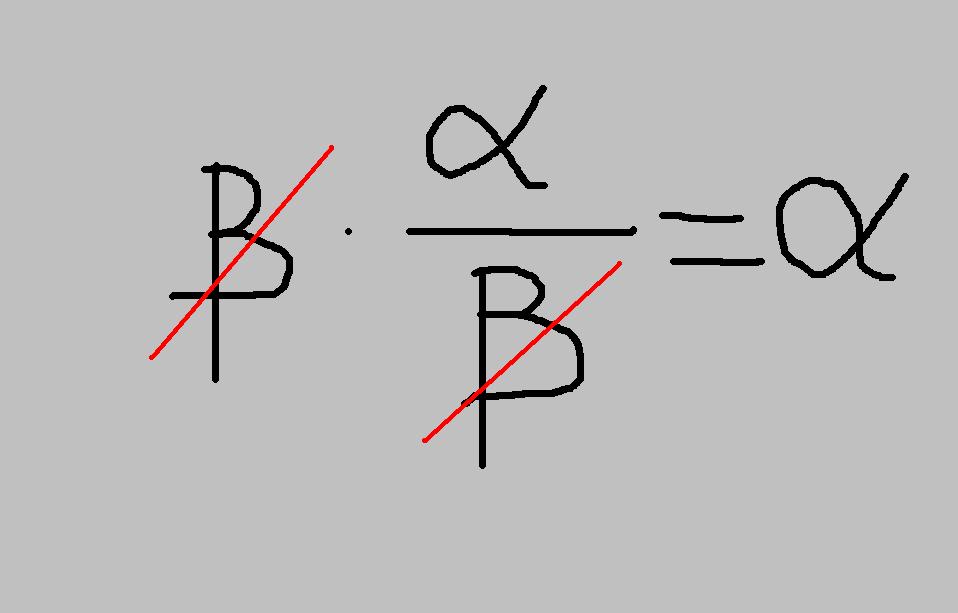Άλγεβρα Β΄ Λυκείου

Γραφική Παράσταση Ευθείας – Khan Academy

Μια σειρά ασκήσεων από Khan Academy στην ενότητα Εξίσωση Ευθείας
[khan_exercise src=’static:graphing_linear_equations’ /]

Θέλω να μάθω … πως λύνεται μια εξίσωση 1ου βαθμού

Μεθοδολογία επίλυσης εξίσωσης 1ου βαθμού και λυμένο παράδειγμα.

Κατ’ αρχάς να ξεκινήσουμε από τον τίτλο του άρθρου που είναι λάθος, γιατί αυτό που θα δούμε σ αυτή τη δημοσίευση είναι η διαδικασία που ακολουθούμε ώστε να βρούμε τη λύση μιας εξίσωσης 1ου βαθμού και αυτή (η διαδικασία) λέγεται επίλυση κι όχι λύση (το τι είναι λύση το έχουμε γράψει εδώ).

Ας δούμε λοιπόν ποια βήματα πρέπει να ακολουθούμε ώστε να βρίσκουμε σε οποιαδήποτε εξίσωση 1ου βαθμού, αν έχει λύση και ποια είναι αυτή ή αν δεν έχει λύσεις (αδύνατη). Σκοπός μας είναι μέσα από τη διαδικασία που θα ακολουθήσουμε, σε οποιαδήποτε πρωτοβάθμια εξίσωση κι αν μας έχει δοθεί, να καταλήξουμε στη πιό απλή μορφή εξίσωσης που υπάρχει και είναι αυτή:

$\alpha\cdot\chi=\beta$ , όπου το $\alpha$ και το $\beta$ μπορεί να είναι οποιοσδήποτε αριθμός

Με τέσσερα απλά βήματα (στη χειρότερη περίπτωση) μπορούμε να καταλήξουμε στη μορφή $\alpha\cdot\chi=\beta$ . Τα βήματα είναι τα παρακάτω που θα τα δούμε λύνοντας ταυτόχρονα κι ένα παράδειγμα:

Continue reading «Θέλω να μάθω … πως λύνεται μια εξίσωση 1ου βαθμού»

Θέλω να μάθω…πως διώχνω τους παρονομαστές από μια εξίσωση

Απαλοιφή παρονομαστών

Η διαδικασία που ακολουθούμε ώστε να «διώξουμε» τους παρονομαστές από μια ισότητα, λέγεται απαλοιφή παρονομαστών.

Αν λοιπόν είμαστε άτυχοι κι η εξίσωσή μας έχει παρονομαστές θα πρέπει να τους διώξουμε για να … «κάνουμε τη ζωή μας πιο εύκολη». Το να «εξουδετερώσεις» ή να «εξαφανίσεις» ένα παρονομαστή που εμφανίζεται σε μια ισότητα (ή σε μια εξίσωση, αφού κι αυτή ισότητα είναι) είναι πολύ εύκολη υπόθεση , αρκεί ένας πολλαπλασιασμός.

Για να διώξεις για παράδειγμα τον παρονομαστή 2, αρκεί να πολλαπλασιάσεις όλους τους όρους της ισότητας (στο πρώτο και στο δεύτερο μέλος) με το 2. Δείτε ένα παράδειγμα,

η $x+\frac{3}2=5x$ πολλαπλασιαζόμενη με το 2 γίνεται

$2x+2\cdot\frac{3}2=2\cdot5x$

$\Leftrightarrow2x+3=10x$

που είναι πλέον απαλλαγμένη από παρονομαστές.

Είναι προφανές ότι μπορούσαμε να πετύχουμε το σκοπό μας πολλαπλασιάζοντας όχι μόνο με το 2 αλλά με οποιοδήποτε από τα πολλαπλάσια του 2 όπως 4,6,8,…, επιλέξαμε όμως το μικρότερο για να έχουμε στην νέα εξίσωση που προκύπτει τους μικρότερους δυνατούς συντελεστές. Επίσης είναι προφανές ότι αν ήθελα να «εξαφανίσω» το 3, το 5 κ.ο.κ. από κάποιον παρονομαστή θα διάλεγα να πολλαπλασιάσω με το 3 ή το 5 αντίστοιχα.

Ένα εύλογο ερώτημα που μπαίνει εδώ είναι τι θα κάναμε αν είχαμε δύο ή περισσότερους διαφορετικούς παρονομαστές; Ας υποθέσουμε ότι θέλουμε να εξουδετερώσουμε το 2 και το 3. Η απάντηση είναι απλή και λογική (όπως απλά και λογικά είναι πάντα τα μαθηματικά): Θα πολλαπλασιάζαμε και με το 2 και με το 3 ταυτόχρονα, ή με άλλα λόγια θα πολλαπλασιάζαμε με το 6 (6 = 2.3). Και πάλι τονίζουμε ότι τη δουλεία μας μπορούσαμε να τη κάνουμε όχι μόνο με το 6 αλλά και με τους 12,18,24,…(πολλαπλάσια του 6) δηλαδή με κάθε κοινό πολλαπλάσιο των παρονομαστών 2 και 3. Εμείς όμως διαλέγουμε το μικρότερο κοινό πολλαπλάσιο, το Ε.Κ.Π. δηλαδή, γιατί «έτσι μας συμφέρει». Δείτε το,

$\frac{x}3+\frac{3}2=5x\Leftrightarrow$

$2\cdot3\cdot\frac{x}3+2\cdot3\cdot\frac{3}2=2\cdot3\cdot5x\Leftrightarrow$

$2x+3\cdot3=2\cdot3\cdot5x\Leftrightarrow$

$2x+9=30x$

Επομένως συνοψίζοντας,

[gn_box title=»tip» type=»info»] για να διώξουμε τους παρονομαστές από μια εξίσωση, πολλαπλασιάζουμε όλους τους όρους της εξίσωσης με το Ε.Κ.Π. των παρονομαστών.[/gn_box]

Θέλω να μάθω … πότε μια εξίσωση λέγεται αδύνατη και πότε αόριστη

Στο προηγούμενο άρθρο μας αναφέραμε ότι εξίσωση είναι μια ισότητα που περιέχει τουλάχιστον μια μεταβλητή (ένα γράμμα που συνήθως αποκαλούμε άγνωστο) και ότι λύση ή ρίζα της εξίσωσης λέμε τον αριθμό που επαληθεύει την εξίσωση (δηλαδή τον αριθμό που αν πάρει τη θέση του γράμματος θα προκύψει μια αληθής ισότητα.
Επίσης είχαμε αναφέρει ότι μια εξίσωση μπορούμε να την θεωρούμε σαν μια ερωτηματική πρόταση σαν μια ερώτηση δηλαδή. Αλλά όπως θα έχετε παρατηρήσει κάποιες ερωτήσεις έχουν απαντήσεις (μία ή περισσότερες ) και κάποιες δεν έχουν. Ας δούμε λίγα παραδείγματα:

Ερώτηση	Απάντηση	Αριθμός Απαντήσεων
Ποια μέρα της εβδομάδας έχει 10 γράμματα;	Δεν υπάρχει	0
Πόσες είναι οι μέρες της εβδομάδας;	7	1
Ποιοι είναι οι καλοκαιρινοί μήνες;	Ιούνιος, Ιούλιος, Αύγουστος	3
Ποια χρονιά έχει 12 μήνες;	Όλες	Όποιον φυσικό αριθμό και να δώσετε ως απάντηση θεωρείται σωστό

Το ίδιο συμβαίνει και με τις εξισώσεις,

Continue reading «Θέλω να μάθω … πότε μια εξίσωση λέγεται αδύνατη και πότε αόριστη»

Θέλω να μάθω…τι είναι η εξίσωση

Η γλώσσα των μαθηματικών

math_symbols — Κάνε κλικ στην εικόνα αν θες να δεις κι άλλα σύμβολα

Τα μαθηματικά είναι μια γλώσσα και όπως όλες οι γλώσσες χρησιμοποιεί κι αυτή σύμβολα. Για να μπορέσουμε να κατανοήσουμε λοιπόν μια γλώσσα θα πρέπει να μάθουμε τι εκφράζουν τα σύμβολα που αυτή χρησιμοποιεί. Άλλα σύμβολα είναι απλά, όπως τα γράμματα και οι αριθμοί που συνδυαζόμενα μεταξύ τους μας δίνουν τις λέξεις και τις προτάσεις και άλλα είναι πιο σύνθετα και μας δίνουν κάποιες εντολές, πληροφορίες κ.α. (π.χ. τα εισαγωγικά «» που μας πληροφορούν ότι ό,τι υπάρχει μέσα σε αυτά ειπώθηκε ακριβώς κατά αυτό τον τρόπο ή το Km που δηλώνει ένα συγκεκριμένο μήκος κ.α.). Τα πιο συνηθισμένα σύμβολα στα μαθηματικά μάλλον είναι τα σύμβολα των τεσσάρων πράξεων (+,-,●,:) και τα σύμβολα της ισότητας ( = ) και της ανισότητας ( < , >, $\le$ , $\ge$ ).

Σωστό ή λάθος;

Με τα σύμβολα όπως προαναφέραμε φτιάχνουμε λέξεις και προτάσεις. Για παράδειγμα,

Η Ελλάδα είναι μια Ευρωπαϊκή χώρα. (πρόταση 1 )

Ο Ιούλιος είναι ο έκτος μήνας του χρόνου. ( πρόταση 2 )

Ποια είναι η πρωτεύουσα της Ιταλίας; (πρόταση 3 )

Όπως φαίνεται από τα παραπάνω παραδείγματα υπάρχουν Continue reading «Θέλω να μάθω…τι είναι η εξίσωση»

Προσδιορισμός του Συντελεστή Διεύθυνσης της Ευθείας

Δείτε με ποιους τρόπους μπορούμε να υπολογίσουμε το συντελεστή διεύθυνσης μιας ευθείας ανάλογα με τα δεδομένα της άσκησης. Το άρθρο απευθύνεται σε μαθητές της Β΄ Λυκείου και κυρίως σε αυτούς που παρακολουθούν την θετική ή την τεχνολογική κατεύθυνση.

Σε προηγούμενο άρθρο είδαμε πως μπορούμε να βρούμε την εξίσωση μιας ευθείας. Είχαμε αναφέρει λοιπόν ότι πρέπει να μας έχουν δοθεί οπωσδήποτε ο συντελεστής διεύθυνσης (λ) κι ένα σημείο Α(χ_Α,ψ_Α) της ευθείας. Μάλιστα είχαμε λύσει κι ένα παράδειγμα όπου και τα δύο (συντελεστής και σημείο) δίνονταν άμεσα. Σήμερα θα δούμε με ποιους τρόπους θα μπορούσαν να μας δώσουν (έμμεσα) το συντελεστή διεύθυνσης.

Μέσω της γωνίας που σχηματίζει η ευθεία με τον άξονα χ΄χ:
Αν η ευθεία (ε) η οποία ζητάμε σχηματίζει γωνία ω με τον άξονα χ΄χ, τότε ισχύει: λ_ε=εφω
Μέσω δύο σημείων Α και Β από τα οποία διέρχεται η ευθεία:
Έστω ότι η ευθεία (ε) που θέλουμε να βρούμε διέρχεται από τα σημεία Α(x_A,y_Α) και Β(x_Β,y_Β), τότε για το συντελεστή διεύθυνσης λ_ετης ευθείας (ε) ισχύει:
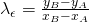$\lambda_\epsilon=\frac{y_B-y_A}{x_B-x_A}$ (μόνο για το Λύκειο)
Μέσω της παραλληλίας της ζητούμενης ευθείας με μια άλλη ευθεία που μας έχουν δώσει:
Αν η ευθεία (ε) που ψάχνουμε είναι παράλληλη με μια ευθεία (δ) μας έχουν δώσει, τότε ισχύει: λ_ε = λ_δ.
Μέσω της καθετότητας της ζητούμενης ευθείας με άλλη ευθεία που μας έχει δοθεί:
Αν η ζητούμενη ευθεία (ε) είναι κάθετη σε δοσμένη ευθεία (δ), τότε ισχύει: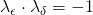 $\lambda_\epsilon\cdot\lambda_\delta=-1$
Μέσω της παραλληλίας της ζητούμενης ευθείας με ένα διάνυσμα που μας έχουν δώσει (Β΄ Λυκείου Κατεύθυνση):
Αν η ευθεία που αναζητάμε είναι παράλληλη με ένα διάνυσμα που μας έχουν δώσει με συντελεστή λ_δ, τότε ισχύει: λ_ε = λ_δ.
Μέσω της καθετότητας της ζητούμενης ευθείας με ένα διάνυσμα που μας έχει δοθεί (Β΄ Λυκείου κατεύθυνση):
Αν η ευθεία μας είναι κάθετη σε κάποιο διάνυσμα που έχει συντελεστή διεύθυνσης λ_δ, τότε θα ισχύει: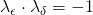 $\lambda_\epsilon\cdot\lambda_\delta=-1$ .

Συγκεντρώνοντας όλα τα παραπάνω σε ένα πίνακα έχουμε:

Eυθεία (ε) με…	Υπολογισμός του λ_ε
(ε) και χ΄χ να σχηματίζουν γωνία ω	λ_ε = εφω
(ε) να διέρχεται από Α(x_A,y_A) και Β(x_B,Y_B)	$\lambda_\epsilon=\frac{y_B-y_A}{x_B-x_A}$
(ε) παράλληλη προς την ευθεία (δ)	λ_ε = λ_δ
(ε) κάθετη με την ευθεία (δ)	$\lambda_\epsilon\cdot\lambda_\delta=-1$
(ε) παράλληλη με το διάνυσμα	λ_ε = λ_δ
(ε) κάθετη με το διάνυσμα	$\lambda_\epsilon\cdot\lambda_\delta=-1$

Και για να ολοκληρώσουμε αυτά που είχαμε πει για τον προσδιορισμό της εξίσωσης μιας ευθείας θα τελειώσουμε βλέποντας με ποιο άλλο τρόπο θα μπορούσαν να μας δώσουν ένα σημείο από το οποίο περνά η ευθεία. Αν λοιπόν δεν δοθεί άμεσα θα μπορούσε να δοθεί ως τομή δύο άλλων ευθειών. Στην περίπτωση αυτή για να βρούμε τις συντεταγμένες του σημείου που χρειαζόμαστε πρέπει να λύσουμε το σύστημα αυτών των δύο εξισώσεων (αυτό θα μπορούσε να γίνει μόνο για τις Γ΄ Γυμνασίου, Α΄ Λυκείου και στην Κατεύθυνση της Β΄ Λυκείου. Στη Β΄ Γυμνασίου το σημείο θα δίνεται άμεσα.

Επειδή το άρθρο είναι σχετικά μεγάλο τα απαραίτητα παραδείγματα θα τα λύσουμε στο επόμενο.

Συνεχίζεται…>>>

Η εξίσωση της Ευθείας

Η εξίσωση ψ=λχ+β είναι γνωστό ότι παριστάνει μια ευθεία. Όμως ποιος ο ρόλος του λ και ποιος του β στην εξίσωση αυτή;

Είναι γνωστό ότι η αλγεβρική μορφή της εξίσωσης μιας ευθείας είναι η

Γραφική παράσταση — Κάντε κλικ στην εικόνα να δείτε το ρόλο των λ και β

$y=\lambda\cdot\chi+\beta$ $(\epsilon)$ , όπου

ο (πραγματικός) αριθμός λ ονομάζεται «συντελεστής διεύθυνσης» και εκφράζει την κλίση της ευθείας σε σχέση με τονημιάξονα Οχ και
ο αριθμός β δηλώνει τη θέση πάνω στον άξονα ψ΄ψ από την οποία διέρχεται η ευθεία.

Αυτό με το οποίο θα ασχοληθούμε σήμερα είναι το πως μπορούμε να βρούμε την εξίσωση μιας ευθείας, δηλαδή με άλλα λόγια να υπολογίσουμε τους αριθμούς λ και β.

Για να μπορέσουμε να βρούμε την εξίσωση θα πρέπει οπωσδήποτε να γνωρίζουμε (να μας έχουν δώσει δηλαδή)

το συντελεστή διεύθυνσης (λ) και

ένα σημείο έστω Α(χ_Α,ψ_Α) από το οποίο διέρχεται η ευθεία που ψάχνουμε.

Για παράδειγμα ας βρούμε την ευθεία που έχει συντελεστή διεύθυνσης 2 και διέρχεται από το σημείο Α(1,3).

Λύση:

Η εξίσωση της ευθείας $(\epsilon)$ θα έχει τη μορφή:

$y=\lambda\cdot\chi+\beta$

όμως μας έχουν δώσει ότι το λ=2,

$y=2\cdot\chi+\beta$

Για να δούμε τώρα πως θα υπολογίσουμε το β.

Έχουμε αναφέρει σε προηγούμενο άρθρο ότι,

«Όταν η γραφική παράσταση μιας συνάρτησης διέρχεται από κάποιο σημείο, τότε οι συντεταγμένες του σημείου επαληθεύουν την εξίσωση (τον τύπο) της συνάρτησης αυτής»

κι έτσι

[warning]Όταν μας δίνουν εξίσωση ευθείας και σημείο από το οποίο διέρχεται η ευθεία αυτή πάντα αντικαθιστούμε τις συντεταγμένες του σημείου στην εξίσωση της ευθείας.[/warning]

Ας το εφαρμόσουμε στην συγκεκριμένη περίπτωση να δούμε. Αντικαθιστούμε λοιπόν το χ με τον αριθμό 1 και το ψ με τον αριθμό 3 κι έχουμε:

$y=2\cdot\chi+\beta$ ,για χ=1 και y=3

$3=2\cdot1+\beta$

προέκυψε λοιπόν μια εξίσωση με μοναδικό άγνωστο το β, το οποίο και υπολογίζουμε

$3-2=\beta\Leftrightarrow\beta=1$

Βρήκαμε λοιπόν ότι η ευθεία με συντελεστή διεύθυνσης λ=2 που διέρχεται από το σημείο Α(1,3) είναι η

y=2x+1.

Σχόλια:

Θυμηθείτε τι έχουμε αναφέρει προηγούμενα » όσα πράγματα μας ζητούν τόσα πρέπει και να μας δίνουν γιαυτό αναζητήστε τα στην εκφώνηση της άσκησης.

[notice]

Tip 1:

Πλήθος Ζητούμενων = Πλήθος Δεδομένων

[/notice]

Αυτή την άσκηση είμαι σίγουρος ότι θα την χαρακτηρίσετε ως εύκολη. Σας πληροφορώ όμως ότι είναι η μοναδική κατηγορία ασκήσεων στην αναζήτηση της εξίσωσης μιας ευθείας. Οποιαδήποτε άλλη κι αν δείτε δεν έχει τίποτα παραπάνω τίποτα λιγότερο. Αυτό που κάνει κάποιες ασκήσεις της κατηγορίας αυτής πιο σύνθετες είναι ο τρόπος με τον οποίο δίνονται τα απαραίτητα στοιχεία δηλαδή ο συντελεστής διεύθυνσης και το σημείο.
Ακριβώς στο επόμενο άρθρο μας θα δούμε αυτό ακριβώς το «παιχνίδι», με ποιους τρόπους είναι δυνατό να δοθεί (έμμεσα) το λ και με ποιους τρόπους το σημείο.

[important]

Tip 2:

Για να βρούμε την εξίσωση μιας ευθείας πρέπει απαραίτητα να μας δίνουν (άμεσα ή έμμεσα)

[gn_list style=»guard»]

το συντελεστή διεύθυνσης
ένα σημείο της.

[/gn_list]

[/important]

Μέχρι τότε μπορείτε εσείς να δοκιμάσετε να λύσετε την παρακάτω άσκηση και να μας στείλετε την απάντηση (στα σχόλια του άρθρου) καθώς κι οποιαδήποτε απορία έχετε, ή κάποιο σχόλιο που θέλετε να κάνετε.

Μπορείτε φυσικά να επικοινωνήσετε και με e-mail.

Άσκηση:

Να βρεθεί η ευθεία (3) που έχει συντελεστή διεύθυνσης διπλάσιο από τον συντελεστή διεύθυνσης της ευθείας (δ):2ψ+4χ=3 αν γνωρίζετε ότι το σημείο Α(-3,8) είναι σημείο της (ε).

Συνεχίζεται…>>>