Απαλοιφή παρονομαστών
Η διαδικασία που ακολουθούμε ώστε να «διώξουμε» τους παρονομαστές από μια ισότητα, λέγεται απαλοιφή παρονομαστών.
Αν λοιπόν είμαστε άτυχοι κι η εξίσωσή μας έχει παρονομαστές θα πρέπει να τους διώξουμε για να … «κάνουμε τη ζωή μας πιο εύκολη». Το να  «εξουδετερώσεις» ή να «εξαφανίσεις» ένα παρονομαστή που εμφανίζεται σε μια ισότητα (ή σε μια εξίσωση, αφού κι αυτή ισότητα είναι) είναι πολύ εύκολη υπόθεση , αρκεί ένας πολλαπλασιασμός.
«εξουδετερώσεις» ή να «εξαφανίσεις» ένα παρονομαστή που εμφανίζεται σε μια ισότητα (ή σε μια εξίσωση, αφού κι αυτή ισότητα είναι) είναι πολύ εύκολη υπόθεση , αρκεί ένας πολλαπλασιασμός.
Για να διώξεις για παράδειγμα τον παρονομαστή 2, αρκεί να πολλαπλασιάσεις όλους τους όρους της ισότητας (στο πρώτο και στο δεύτερο μέλος) με το 2. Δείτε ένα παράδειγμα,
η ![]() πολλαπλασιαζόμενη με το 2 γίνεται
πολλαπλασιαζόμενη με το 2 γίνεται
![]()
![]()
που είναι πλέον απαλλαγμένη από παρονομαστές.
Είναι προφανές ότι μπορούσαμε να πετύχουμε το σκοπό μας πολλαπλασιάζοντας όχι μόνο με το 2 αλλά με οποιοδήποτε από τα πολλαπλάσια του 2 όπως 4,6,8,…, επιλέξαμε όμως το μικρότερο για να έχουμε στην νέα εξίσωση που προκύπτει τους μικρότερους δυνατούς συντελεστές. Επίσης είναι προφανές ότι αν ήθελα να «εξαφανίσω» το 3, το 5 κ.ο.κ. από κάποιον παρονομαστή θα διάλεγα να πολλαπλασιάσω με το 3 ή το 5 αντίστοιχα.
Ένα εύλογο ερώτημα που μπαίνει εδώ είναι τι θα κάναμε αν είχαμε δύο ή περισσότερους διαφορετικούς παρονομαστές; Ας υποθέσουμε ότι θέλουμε να εξουδετερώσουμε το 2 και το 3. Η απάντηση είναι απλή και λογική (όπως απλά και λογικά είναι πάντα τα μαθηματικά): Θα πολλαπλασιάζαμε και με το 2 και με το 3 ταυτόχρονα, ή με άλλα λόγια θα πολλαπλασιάζαμε με το 6 (6 = 2.3). Και πάλι τονίζουμε ότι τη δουλεία μας μπορούσαμε να τη κάνουμε όχι μόνο με το 6 αλλά και με τους 12,18,24,…(πολλαπλάσια του 6) δηλαδή με κάθε κοινό πολλαπλάσιο των παρονομαστών 2 και 3. Εμείς όμως διαλέγουμε το μικρότερο κοινό πολλαπλάσιο, το Ε.Κ.Π. δηλαδή, γιατί «έτσι μας συμφέρει». Δείτε το,
![]()
![]()
![]()
![]()
Επομένως συνοψίζοντας,
[gn_box title=»tip» type=»info»] για να διώξουμε τους παρονομαστές από μια εξίσωση, πολλαπλασιάζουμε όλους τους όρους της εξίσωσης με το Ε.Κ.Π. των παρονομαστών.[/gn_box]

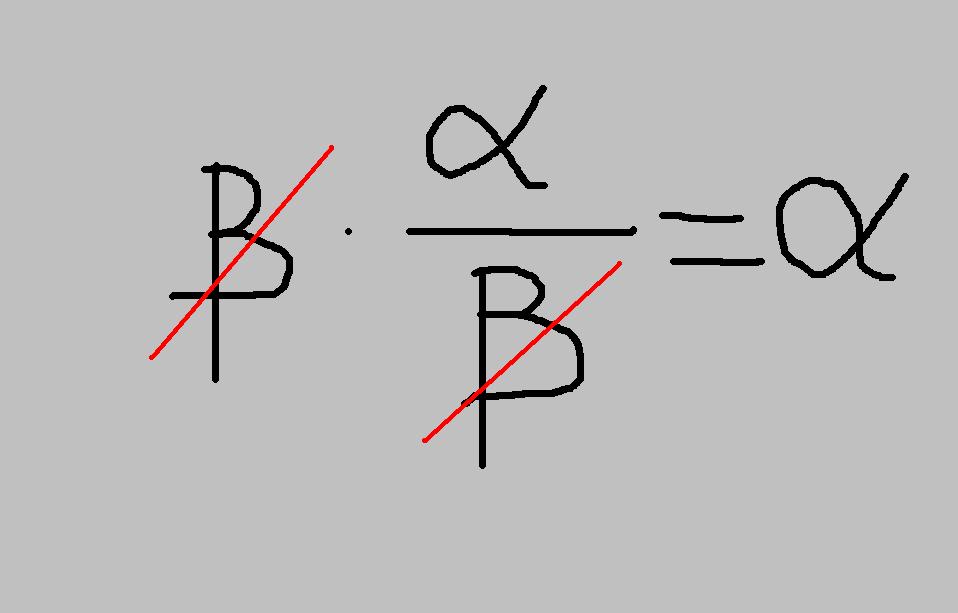
και αν εχουμε 1/4= (2+λ/3 + 1+λ/2) ? τοτε πως κανουμε απαλοιφη στη παρενθεση…
Η εξίσωση που έχεις Αντρέα έχει παρονομαστές τους αριθμούς 2,3 και 4 ο μικρότερος αριθμός που μπορούμε να χρησιμοποιήσουμε για να διώξουμε τους παρονομαστές αυτούς είναι το Ε.Κ.Π. τους που είναι το 12. Έτσι λοιπόν θα έχουμε:
Οι παρονομαστές εξαφανίστηκαν και εξίσωση τώρα λύνεται κάνοντας χρήση της επιμεριστικής ιδιότητας (για να απαλλαγούμε κι από τις παρενθέσεις)
Για να μπορέσω να συνεχίσω τις πράξεις αναγκάζομαι τώρα να μεταφέρω τους γνωστούς στο ένα μέλος και τους άγνωστους στο άλλο, οπότε προκύπτει
και τελικά έχουμε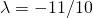
Η διαδικασία που ακολουθήσαμε για να λύσουμε αυτήν την εξίσωση βρίσκεται εδώ
na rotisw kati parakalw… den exw katalavi akoma pos vriskis to elaxisto kino polaplasio … borei na mu e3igisei kaneis?tora 8a bo 1 gimnasiu kai 8elw na ta 3erw kala..:)
Εγω παω τωρα Α’ Γυμνασιου. Ειναι πολυ απλο, θα σου το κανω με παραδειγμα γιατι στη θεωρια δεν το ‘χω ιδιαιτερα. Εχεις να βρεις π.χ. ΕΚΠ(25, 30, 50)=
Εγω να ρωτησω κατι?
Αν ο αγνωστος ειναι παρονομαστης, τι κανουμε?
Δήμητρα, μπράβο σου που απάντησες στο προηγούμενο σχόλιο (γιατί εγώ δεν το είχα προσέξει και το άφησα αναπάντητο) και μάλιστα απάντησες πολύ σωστά. Όσον αφορά τώρα στην απορία που έχεις, στην Α΄Γυμνασίου το μόνο που μπορείς να κάνεις είναι τη μέθοδο «χιαστί». Κι αυτό γιατί οι εξισώσεις που θα πρέπει να λύσεις θα είναι της μορφής:
πολλαπλασιάζεις «χιαστί» και παίρνεις:
δηλαδή,
κι αφού τα 4x κάνουν 48 το ένα x που μας ενδιαφέρει εμάς θα είναι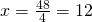 .
.
mpravo panagioti . egw eimai ma8htria ths b gymnasiou . to septembrio 8a paw 3 gymnasiou.. latrevw ta ma8hmatika…
Σ’ ευχαριστώ Στέφι κι εγώ τα λατρεύω
Εγω θα ηθελα να ρωτησω τι κανει κανεις στην περιπτωση πιο συνθετης εξισωσης οπως αυτη: ((α-βi)/(β+αi))^v +((β-αi)/(α+βi))^ν
Γιάννη αυτό που γράφεις αφορά μιγαδικούς. Ρίξε μια ματιά εδώ:Μιγαδικοί
Συγνωμη που ρωταω αλλα χρειαζομαι την βοηθεια σας…. Αν εχουμε την εξισωση: 2×-5=4χ-3/5 τι κανουμε;; πολλαπλασιαζουμε με το 5;;
Ναι
χ+1=-χ+2
___ ____
2 4
Στην ισότητα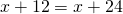 έχεις δύο παρονομαστές το 2 και το 4, αν πολλαπλασιάσεις με το 4 και τα δύο μέλη θα απλοποιηθούν οι παρονομαστές:
έχεις δύο παρονομαστές το 2 και το 4, αν πολλαπλασιάσεις με το 4 και τα δύο μέλη θα απλοποιηθούν οι παρονομαστές:
Αυτό συμβαίνει γιατί το 4 που πολλαπλασιάσαμε διαιρείται ακριβώς και με τον παρονομαστή 2 και με τον παρονομαστή 4. Ψάχνεις λοιπόν κάθε φορά έναν κατάλληλο αριθμό που να έχει την ιδιότητα να διαιρείται με όλους τους παρονομαστές. Τέτοιοι αριθμοί είναι άπειροι, στο παράδειγμά μας θα μπορούσαμε να χρησιμοποιήσουμε και το 8, το 12, 16,20,… και γενικά κάθε πολλαπλάσιο του 4. Προτιμήσαμε όμως τον μικρότερο προφανώς για λόγους ευκολίας. Έτσι λοιπόν καταλαβαίνουμε πως είναι προτιμότερο κάθε φορά να βρίσκουμε το Ε.Κ.Π. των παρονομαστών και να χρησιμοποιούμε αυτό.