Συνευθειακά Σημεία
Συνευθειακά Σημεία
(Μαθηματικά Κατεύθυνσης Β΄ Λυκείου)
Μπορούμε να αποδείξουμε ότι τρία σημεία είναι συνευθειακά με τρεις διαφορετικούς τρόπους ανάλογα με το σημείο στο οποίο έχουμε φτάσει στην ύλη μας στο σχολείο (Μαθηματικά Κατεύθυνσης Β΄ Λυκείου).
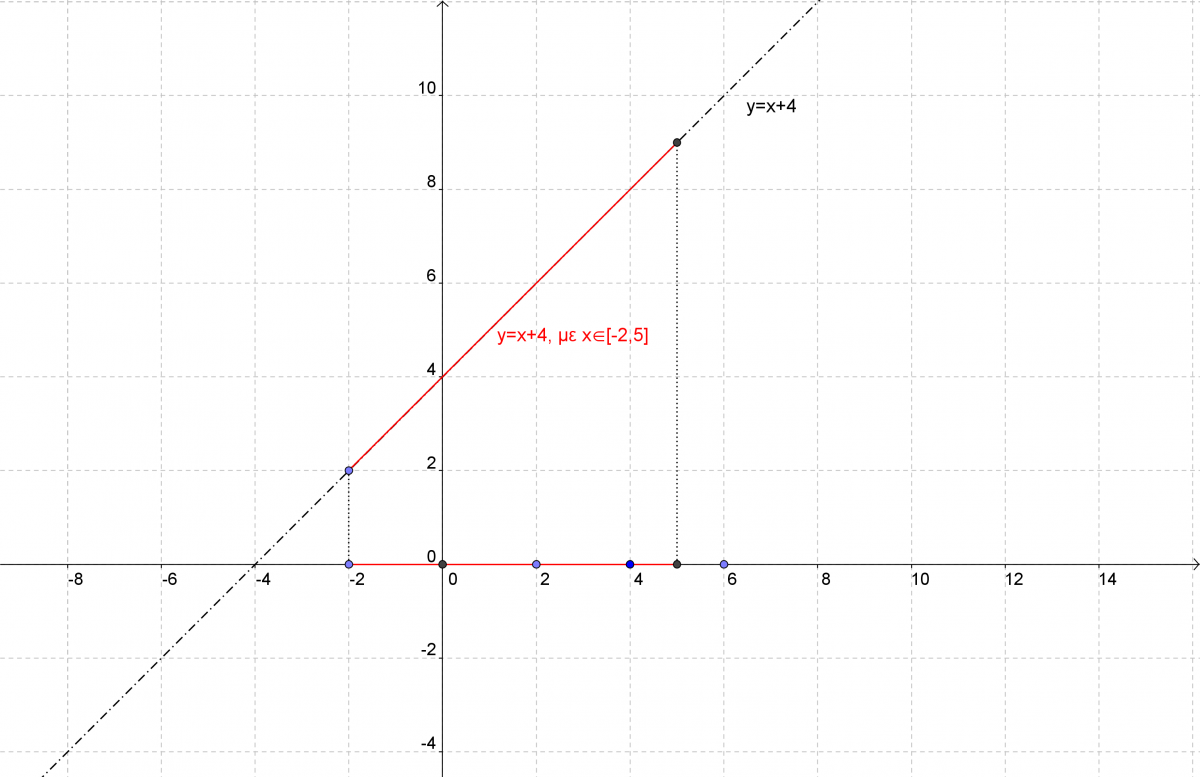
Έστω λοιπόν ότι έχουμε τα σημεία Α(1,3), Β(2,5) και Γ(4,9)
- 1ος τρόπος, με διανύσματα
Κατ’ αρχάς φτιάχνουμε δύο διανύσματα με άκρα αυτά τα σημεία έστω τακαι
(Υπενθύμιση 1η),
και
στη συνέχεια αποδεικνύουμε ότι αυτά τα διανύσματα είναι παράλληλα είτε με τους συντελεστές διεύθυνσης (Υπενθύμιση 2η)
είτε με την ορίζουσα (Υπενθύμιση 3η)
Αυτό όμως ταυτόχρονα μας δείχνει ότι τα σημεία Α,Β και Γ είναι συνευθειακά γιατί για να είναι παράλληλα τα δύο διανύσματα θα πρέπει είτε να βρίσκονται σε παράλληλους φορείς πράγμα αδύνατο αφού έχουν ένα κοινό σημείο, το Β είτε να βρίσκονται στον ίδιο φορέα στην ίδια ευθεία δηλαδή.
[box type=»info»] Υπενθύμιση 1η:
αν και
δύο σημεία τότε το διάνυσμα
[/box]
[box type=»info»] Υπενθύμιση 2η:
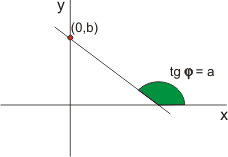
Ένα διάνυσμα έχει συντελεστή διεύθυνσης
εννοείται
[/box]
[box type=»info»] Υπενθύμιση 3η:
[/box]
- 2ος τρόπος, με ευθείες
Με το ίδιο σκεπτικό μπορούμε να δείξουμε ότι τα τρία σημεία βρίσκονται στην ίδια ευθεία αποδεικνύοντας ότι δύο ευθείες από αυτές που διέρχονται από τα Α,Β, και Γ είναι παράλληλες (δηλαδή έχουν τον ίδιο συντελεστή διεύθυνσης).Έτσι λοιπόν βρίσκουμε το συντελεστή διεύθυνσης της ΑΒ και ΒΓ(Υπενθύμιση 4η) κι έχουμεΔύο ευθείες όμως με ένα κοινό σημείο (το Β) δεν γίνεται να είναι παράλληλες. Τι συμβαίνει τότε; Οι δύο ευθείες ταυτίζονται δηλαδή δεν είναι δύο αλλά μόνο μία ευθεία.
[box type=»info»] Υπενθύμιση 4η:
αν μια ευθεία (ε) διέρχεται από τα σημεία και
τότε ο συντελεστής διεύθυνσής της είναι:
[/box]
- 3ος τρόπος, με τρίγωνα

Κάντε κλικ στην εικόνα για να «παίξετε» Αρκεί να δείξουμε ότι το τρίγωνο ΑΒΓ έχει εμβαδό ίσο με 0, γιατί αυτό απλά σημαίνει ότι δεν υπάρχει τρίγωνο ΑΒΓ δηλαδή τα σημεία Α,Β και Γ δεν σχηματίζουν τρίγωνο γιατί βρίσκονται πάνω στην ίδια ευθεία (συνευθειακά). Έτσι λοιπόν στο παράδειγμά μας έχουμε
που ισχύει (τις πράξεις τις κάναμε προηγούμενα στον 1ο τρόπο).