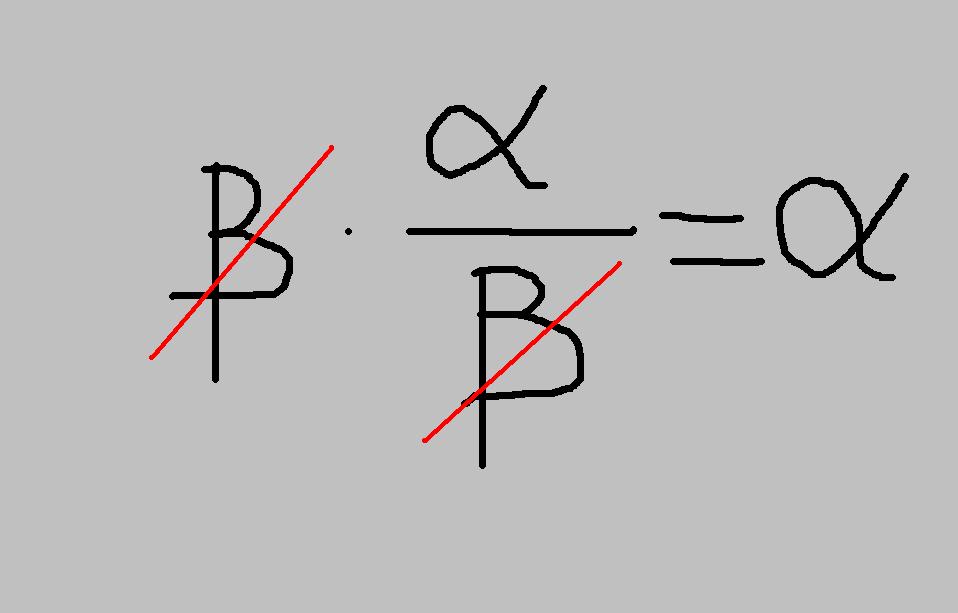Θέλω να μάθω…πως διώχνω τους παρονομαστές από μια εξίσωση

Απαλοιφή παρονομαστών

Η διαδικασία που ακολουθούμε ώστε να «διώξουμε» τους παρονομαστές από μια ισότητα, λέγεται απαλοιφή παρονομαστών.

Αν λοιπόν είμαστε άτυχοι κι η εξίσωσή μας έχει παρονομαστές θα πρέπει να τους διώξουμε για να … «κάνουμε τη ζωή μας πιο εύκολη». Το να «εξουδετερώσεις» ή να «εξαφανίσεις» ένα παρονομαστή που εμφανίζεται σε μια ισότητα (ή σε μια εξίσωση, αφού κι αυτή ισότητα είναι) είναι πολύ εύκολη υπόθεση , αρκεί ένας πολλαπλασιασμός.

Για να διώξεις για παράδειγμα τον παρονομαστή 2, αρκεί να πολλαπλασιάσεις όλους τους όρους της ισότητας (στο πρώτο και στο δεύτερο μέλος) με το 2. Δείτε ένα παράδειγμα,

η $x+\frac{3}2=5x$ πολλαπλασιαζόμενη με το 2 γίνεται

$2x+2\cdot\frac{3}2=2\cdot5x$

$\Leftrightarrow2x+3=10x$

που είναι πλέον απαλλαγμένη από παρονομαστές.

Είναι προφανές ότι μπορούσαμε να πετύχουμε το σκοπό μας πολλαπλασιάζοντας όχι μόνο με το 2 αλλά με οποιοδήποτε από τα πολλαπλάσια του 2 όπως 4,6,8,…, επιλέξαμε όμως το μικρότερο για να έχουμε στην νέα εξίσωση που προκύπτει τους μικρότερους δυνατούς συντελεστές. Επίσης είναι προφανές ότι αν ήθελα να «εξαφανίσω» το 3, το 5 κ.ο.κ. από κάποιον παρονομαστή θα διάλεγα να πολλαπλασιάσω με το 3 ή το 5 αντίστοιχα.

Ένα εύλογο ερώτημα που μπαίνει εδώ είναι τι θα κάναμε αν είχαμε δύο ή περισσότερους διαφορετικούς παρονομαστές; Ας υποθέσουμε ότι θέλουμε να εξουδετερώσουμε το 2 και το 3. Η απάντηση είναι απλή και λογική (όπως απλά και λογικά είναι πάντα τα μαθηματικά): Θα πολλαπλασιάζαμε και με το 2 και με το 3 ταυτόχρονα, ή με άλλα λόγια θα πολλαπλασιάζαμε με το 6 (6 = 2.3). Και πάλι τονίζουμε ότι τη δουλεία μας μπορούσαμε να τη κάνουμε όχι μόνο με το 6 αλλά και με τους 12,18,24,…(πολλαπλάσια του 6) δηλαδή με κάθε κοινό πολλαπλάσιο των παρονομαστών 2 και 3. Εμείς όμως διαλέγουμε το μικρότερο κοινό πολλαπλάσιο, το Ε.Κ.Π. δηλαδή, γιατί «έτσι μας συμφέρει». Δείτε το,

$\frac{x}3+\frac{3}2=5x\Leftrightarrow$

$2\cdot3\cdot\frac{x}3+2\cdot3\cdot\frac{3}2=2\cdot3\cdot5x\Leftrightarrow$

$2x+3\cdot3=2\cdot3\cdot5x\Leftrightarrow$

$2x+9=30x$

Επομένως συνοψίζοντας,

[gn_box title=»tip» type=»info»] για να διώξουμε τους παρονομαστές από μια εξίσωση, πολλαπλασιάζουμε όλους τους όρους της εξίσωσης με το Ε.Κ.Π. των παρονομαστών.[/gn_box]

Θέλω να μάθω … πότε μια εξίσωση λέγεται αδύνατη και πότε αόριστη

Στο προηγούμενο άρθρο μας αναφέραμε ότι εξίσωση είναι μια ισότητα που περιέχει τουλάχιστον μια μεταβλητή (ένα γράμμα που συνήθως αποκαλούμε άγνωστο) και ότι λύση ή ρίζα της εξίσωσης λέμε τον αριθμό που επαληθεύει την εξίσωση (δηλαδή τον αριθμό που αν πάρει τη θέση του γράμματος θα προκύψει μια αληθής ισότητα.
Επίσης είχαμε αναφέρει ότι μια εξίσωση μπορούμε να την θεωρούμε σαν μια ερωτηματική πρόταση σαν μια ερώτηση δηλαδή. Αλλά όπως θα έχετε παρατηρήσει κάποιες ερωτήσεις έχουν απαντήσεις (μία ή περισσότερες ) και κάποιες δεν έχουν. Ας δούμε λίγα παραδείγματα:

Ερώτηση	Απάντηση	Αριθμός Απαντήσεων
Ποια μέρα της εβδομάδας έχει 10 γράμματα;	Δεν υπάρχει	0
Πόσες είναι οι μέρες της εβδομάδας;	7	1
Ποιοι είναι οι καλοκαιρινοί μήνες;	Ιούνιος, Ιούλιος, Αύγουστος	3
Ποια χρονιά έχει 12 μήνες;	Όλες	Όποιον φυσικό αριθμό και να δώσετε ως απάντηση θεωρείται σωστό

Το ίδιο συμβαίνει και με τις εξισώσεις,

Continue reading «Θέλω να μάθω … πότε μια εξίσωση λέγεται αδύνατη και πότε αόριστη»

Θέλω να μάθω…τι είναι η εξίσωση

Η γλώσσα των μαθηματικών

math_symbols — Κάνε κλικ στην εικόνα αν θες να δεις κι άλλα σύμβολα

Τα μαθηματικά είναι μια γλώσσα και όπως όλες οι γλώσσες χρησιμοποιεί κι αυτή σύμβολα. Για να μπορέσουμε να κατανοήσουμε λοιπόν μια γλώσσα θα πρέπει να μάθουμε τι εκφράζουν τα σύμβολα που αυτή χρησιμοποιεί. Άλλα σύμβολα είναι απλά, όπως τα γράμματα και οι αριθμοί που συνδυαζόμενα μεταξύ τους μας δίνουν τις λέξεις και τις προτάσεις και άλλα είναι πιο σύνθετα και μας δίνουν κάποιες εντολές, πληροφορίες κ.α. (π.χ. τα εισαγωγικά «» που μας πληροφορούν ότι ό,τι υπάρχει μέσα σε αυτά ειπώθηκε ακριβώς κατά αυτό τον τρόπο ή το Km που δηλώνει ένα συγκεκριμένο μήκος κ.α.). Τα πιο συνηθισμένα σύμβολα στα μαθηματικά μάλλον είναι τα σύμβολα των τεσσάρων πράξεων (+,-,●,:) και τα σύμβολα της ισότητας ( = ) και της ανισότητας ( < , >, $\le$ , $\ge$ ).

Σωστό ή λάθος;

Με τα σύμβολα όπως προαναφέραμε φτιάχνουμε λέξεις και προτάσεις. Για παράδειγμα,

Η Ελλάδα είναι μια Ευρωπαϊκή χώρα. (πρόταση 1 )

Ο Ιούλιος είναι ο έκτος μήνας του χρόνου. ( πρόταση 2 )

Ποια είναι η πρωτεύουσα της Ιταλίας; (πρόταση 3 )

Όπως φαίνεται από τα παραπάνω παραδείγματα υπάρχουν Continue reading «Θέλω να μάθω…τι είναι η εξίσωση»

Απαλλαγή από τις Απόλυτες Τιμές

Στο άρθρο αυτό θα δούμε με τη βοήθεια μιας άσκησης τι πρέπει να κάνουμε για να απαλλαγούμε από τις απόλυτες τιμές όταν αυτό είναι απαραίτητο.

Κατ΄αρχάς ας θυμηθούμε πως ορίζεται η απόλυτη τιμή ενός αριθμού:
$|a|=a$ αν a>0
$|a|=0$ αν a=0
$|a|=-a$ αν a<0

Βλέπουμε λοιπόν ότι για να απαλλαγούμε από τα απόλυτα πρέπει να γνωρίζουμε αν το περιεχόμενο της απόλυτης τιμής είναι θετικό, μηδέν ή αρνητικό γιατί σε κάθε περίπτωση ενεργούμε διαφορετικά.

Για παράδειγμα, αν x<3 τότε $|x-3|=-(x-3)=3-x$ κι αυτό γιατί; γιατί μας έχουν δώσει ότι x<3 άρα θα είναι x-3<3-3 $\Leftrightarrow$ x-3<0 (αφαιρέσαμε κι από τα δυο μέλη το 3 ώστε να δημιουργήσουμε στη δοθείσα ανισότητα το περιεχόμενο του απολύτου).

Για να δούμε τώρα μια άσκηση πάνω στο συγκεκριμένο θέμα. Continue reading «Απαλλαγή από τις Απόλυτες Τιμές»

Επανάληψη στη Θεωρία των Μαθηματικών της Β΄ Γυμνασίου

Εξίσωση:

Εξίσωση είναι μια ισότητα που περιέχει τουλάχιστον μια μεταβλητή (έναν άγνωστο).

Ο αριθμός που επαληθεύει την εξίσωση λέγεται ρίζα ή λύση της εξίσωσης.

Μια εξίσωση που δεν έχει λύση λέγεται αδύνατη

Μια εξίσωση που έχει άπειρες λύσεις λέγεται αόριστη ή και ταυτότητα.

Πυθαγόρειο Θεώρημα:

Ορθογώνιο Τρίγωνο, α=υποτείνουσα, β και γ = κάθετες

Το τετράγωνο της υποτείνουσας ορθογωνίου τριγώνου είναι ίσο με το άθροισμα των τετραγώνων των κάθετων πλευρών του.

Δηλαδή ισχύει: αν A=90^o τότε α²=β²+γ²

(Αντίστροφο) Αν σε ένα τρίγωνο το τετράγωνο της μεγαλύτερης πλευράς είναι ίσο με το άθροισμα των τετραγώνων των δύο άλλων πλευρών του, τότε το τρίγωνο είναι ορθογώνιο. Εννοείται ότι υποτείνουσα θα είναι η μεγαλύτερη πλευρά κι επομένως ορθή θα είναι η γωνία που βρίσκεται απέναντι από αυτή.

Δηλαδή ισχύει: αν α²=β²+γ² τότε A=90^o

Τετραγωνική ρίζα:

Τετραγωνική ρίζα ενός μη αρνητικού αριθμού α (συμβολίζεται: $\sqrt\alpha$ ) είναι ένας μη αρνητικός αριθμός ο οποίος αν υψωθεί στο τετράγωνο μας δίνει τον αριθμό α.

Δηλαδή ισχύει: $\left(\sqrt\alpha\right)^2=\alpha$ με $\alpha\geqq 0$

Ιδιότητες: εννοείται και
- $\sqrt0=0$ και $\sqrt1=1$
- $\sqrt{\alpha\beta}=\sqrt\alpha\cdot\sqrt\beta$
- $\sqrt\frac{\alpha}{\beta}=\frac{\sqrt\alpha}{\sqrt\beta}$ $\beta\neq0$
- $\sqrt{\alpha^2}=\left(\sqrt\alpha\right)^2=\alpha$

Τριγωνομετρία:

Εφαπτομένη οξείας γωνίας ορθογωνίου τριγώνου ονομάζουμε το λόγο της απέναντι πλευράς προς την προσκείμενη κάθετη πλευρά.
Δηλαδή,

Όταν αυξάνεται μια οξεία γωνία αυξάνει και η εφαπτομένη της.
Ημίτονο οξείας γωνίας ορθογωνίου τριγώνου είναι ο λόγος της απέναντι πλευράς προς την υποτείνουσα του τριγώνου.
Δηλαδή,
Όταν αυξάνει μια οξεία γωνία αυξάνει και το ημίτονό της.
Το ημίτονο οποιασδήποτε οξείας γωνίας είναι αριθμός μικρότερος του 1, αφού η απέναντι κάθετη πλευρά είναι μικρότερη της υποτείνουσας.
Συνημίτονο οξείας γωνίας ορθογωνίου τριγώνου είναι ο λόγος της προσκείμενης κάθετης πλευράς του τριγώνου προς την υποτείνουσά του.
Δηλαδή,
Όταν μεγαλώνει μια οξεία γωνία μειώνεται το συνημίτονό της.
Το συνημίτονο οποιασδήποτε οξείας γωνίας είναι μικρότερο του 1, αφού η προσκείμενη κάθετη πλευρά του τριγώνου (που βρίσκεται στον αριθμητή) είναι πάντα μικρότερη από την υποτείνουσα (που βρίσκεται στον παρονομαστή).

Ανάλογα ποσά:

Δυο ποσά (x και y) λέγονται ανάλογα όταν πολλαπλασιάζοντας τις τιμές του ενός ποσού με κάποιον αριθμό, πολλαπλασιάζονται και οι αντίστοιχες τιμές του άλλου ποσού με τον ίδιο αριθμό.
Δυο ποσά x και y είναι ανάλογα αν και μόνο αν το πηλίκο των αντίστοιχων τιμών τους είναι σταθερό.
Δηλαδή, x και y ανάλογα αν και μόνο αν ισχύει $\frac{y}{x}=a$ ή $y=ax$
Η γραφική παράσταση της $y=ax$ είναι ευθεία που διέρχεται από την αρχή των αξόνων και σχηματίζει γωνία (ω) με τον ημιάξονα Οx που έχει εφαπτομένη ίση με το α, δηλαδή $a=\epsilon\phi\omega$

Ποσά αντιστρόφως ανάλογα:

Δυο ποσά (x και y) λέμε ότι είναι αντιστρόφως ανάλογα όταν πολλαπλασιάζοντας τις τιμές του ενός ποσού με κάποιον αριθμό, διαιρούνται με τον ίδιο αριθμό οι αντίστοιχες τιμές του άλλου ποσού.
Τα ποσά x και y είναι αντιστρόφως ανάλογα αν και μόνο αν το γινόμενο των αντίστοιχων τιμών τους είναι σταθερό. Δηλαδή, x,y αντίστροφα αν και μόνο αν ισχύει $yx=a$ ή $y=\frac{a}x$
Η γραφική παράσταση της συνάρτησης
$y=\frac{a}x$

αποτελείται από δυο κλάδους και λέγεται «υπερβολή».

Επίκεντρη – Εγγεγραμμένη:

Επίκεντρη λέγεται η γωνία που έχει την κορυφή της στο κέντρο ενός κύκλου.
Το τόξο του κύκλου που περιέχεται στις πλευρές της επίκεντρης το λέμε αντίστοιχο τόξο της επίκεντρης.
Η επίκεντρη γωνία είναι σε μοίρες ίση με το αντίστοιχο τόξο της.
Εγγεγραμμένη σε κύκλο γωνία λέγεται η γωνία που έχει τη κορυφή της σε κύκλο και οι πλευρές της τέμνουν τον κύκλο αυτό.
Το τόξο του κύκλου που βρίσκεται μεταξύ των πλευρών της εγγεγραμμένης γωνίας λέγεται αντίστοιχο τόξο της γωνίας.
Η εγγεγραμμένη γωνία είναι σε μοίρες ίση με το μισό του αντίστοιχου τόξου της.
Κάθε εγγεγραμμένη γωνία που έχει ως αντίστοιχο τόξο ένα ημικύκλιο είναι ορθή. (ή αλλιώς κάθε εγγεγραμμένη που βαίνει σε ημικύκλιο είναι ορθή).
Εγγεγραμμένες στον ίδιο κύκλο (ή σε ίσους κύκλους) γωνίες που έχουν το ίδιο αντίστοιχο τόξο είναι ίσες.
Σχέση Επίκεντρης και Εγγεγραμμένης γωνίας.
Μια επίκεντρη γωνία είναι διπλάσια από κάθε εγγεγραμμένη που έχει το ίδιο αντίστοιχο τόξο με αυτήν.

Κύκλος:

Τύποι στο Κύκλο
Μήκος Κύκλου	$\Gamma=2\cdot\pi\cdot\rho$
Μήκος Τόξου	$S=2\cdot\pi\cdot\rho\cdot\frac{\mu}{360^0}$
Εμβαδό Κύκλου	$E=\pi\cdot\rho^2$
Εμβαδό Κυκλικού Τομέα	$E_\kappa=\pi\cdot\rho^2\cdot\frac{\mu}{360^o}$
Γ:μήκος κύκλου, Ε: εμβαδό κύκλου, S:μήκος τόξου, Ε_κ: εμβαδό κυκλικού τομέα, ρ: ακτίνα, μ: μοίρες τόξου, π=3,14

Εμβαδά Επίπεδων Σχημάτων:

Τύποι Εμβαδών
Τετράγωνο	$E=\alpha^2$
Παραλληλόγραμμο	$E=\beta\cdot\upsilon$
Τρίγωνο	$E=\frac{1}2\cdot\beta\cdot\upsilon$
Τραπέζιο	$E=\frac{1}2\left(\beta_1+\beta_2\right)\cdot\upsilon$
α:πλευρά τετραγώνου, β, β₁, β₂: βάσεις, υ:ύψος

Η θεωρία της Α΄ Γυμνασίου σε 26 ερωτήσεις με τις απαντήσεις τους

Ερώτηση 1
Ποιοι αριθμοί ονομάζονται πρώτοι και ποιοι σύνθετοι; Να δώσετε και παραδείγματα.
«Απάντηση 1»
Όταν ένας αριθμός διαιρείται μόνο με τον εαυτό του και τη μονάδα λέγεται πρώτος. Παράδειγμα:2,3,13,17,..
Ένας αριθμός που δεν είναι πρώτος λέγεται σύνθετος. Παράδειγμα:8,12,35,…
Ερώτηση 2
i. Τι είναι τα κριτήρια διαιρετότητας;
ii. Να γράψετε τα κριτήρια διαιρετότητας για τους αριθμούς 2,3,5 και 9.
«Απάντηση 2»
i. Οι κανόνες με τους οποίους διακρίνουμε αν ένας αριθμός διαιρείται με τους αριθμούς 2,3,4,…,5 κ.τ.λ. λέγονται κριτήρια διαιρετότητας.
ii. Ένας αριθμός διαιρείται με
a. Το 2, όταν λήγει σε 0,2,4,6,8
b. Το 5,όταν λήγει σε 0,5
c. Το 3, όταν το άθροισμα των ψηφιών του είναι 3,6 ή 9
d. Το 9, όταν το άθροισμα των ψηφιών του είναι 9
Ερώτηση 3
Ποια είναι η σειρά με την οποία εκτελούνται οι πράξεις ( προτεραιότητα πράξεων) σε μια αριθμητική παράσταση που
i. Δεν έχει παρενθέσεις
ii. έχει παρενθέσεις

«Απάντηση 3»
Για να υπολογίσουμε την τιμή μιας αριθμητικής παράστασης έχουμε συμφωνήσει να εκτελούμε τις πράξεις με την παρακάτω σειρά:
i. αν δεν υπάρχουν παρενθέσεις:
a. υπολογίζουμε τις δυνάμεις
b. κάνουμε τους πολλαπλασιασμούς και τις διαιρέσεις
c. κάνουμε τις προσθέσεις και τις αφαιρέσεις.
ii. Αν υπάρχουν παρενθέσεις:
εκτελούμε και πάλι τις πράξεις με την παραπάνω σειρά ξεκινώντας όμως πρώτα μέσα από τις παρενθέσεις.
Ερώτηση 4
i. Ποια είναι η βασική μονάδα μέτρησης του μήκους;
ii. Γράψτε τα πολλαπλάσια και τις υποδιαιρέσεις της.
iii. Τι είναι το ναυτικό μίλι;
«Απάντηση 4»
i. Η βασική μονάδα μέτρησης του μήκους είναι το 1 μέτρο (1m)
ii. Τα πολλαπλάσια του μέτρου είναι: δεκάμετρο-εκατόμετρο-χιλιόμετρο.
οι υποδιαιρέσεις του μέτρου είναι: δεκατόμετρο-εκατοστόμετρο-χιλιοστόμετρο.
iii. Το ναυτικό μίλι (ν.μ.) είναι μονάδα μέτρησης του μήκους και χρησιμοποιείται στη ναυτιλία. 1ν.μ.=1852m
Ερώτηση 5
i. Ποια η μονάδα μέτρησης του εμβαδού;
ii. Ποια η μονάδα μέτρησης του όγκου;
iii. Τι είναι το στρέμμα;
iv. Τι είναι το λίτρο;
«Απάντηση 5»
i. Μονάδα μέτρησης του εμβαδού είναι το τετραγωνικό μέτρο ( $m^2$ ), που είναι ένα τετράγωνο με πλευρά 1 μέτρο.
ii. Μονάδα μέτρησης του όγκου είναι το κυβικό μέτρο( $m^3$ ) , που είναι ένας κύβος με ακμή 1 μέτρο.
iii. Στη χώρα μας για τη μέτρηση μεγάλων επιφανειών, κυρίως αγρών και δασικών εκτάσεων, το στρέμμα, που είναι 1000 τ.μ.
iv. Στη περίπτωση που θέλουμε να εκφράσουμε τον όγκο υγρών χρησιμοποιούμε σαν μονάδα μέτρησης το 1 λίτρο (είναι 1/1000 του $m^3$ ). Συνηθισμένη υποδιαίρεση του λίτρου είναι το ml. 1ml=1/1000 του λίτρου (1ml=1 $cm^3$ ).
Ερώτηση 6
Πότε δύο ή περισσότερα κλάσματα λέγονται ομώνυμα και πότε ετερώνυμα;
«Απάντηση 6»
Δύο ή περισσότερα κλάσματα που έχουν τον ίδιο παρονομαστή λέγονται ομώνυμα. Τα κλάσματα που έχουν διαφορετικούς παρονομαστές λέγονται ετερώνυμα.
Ερώτηση 7
i. Πως συγκρίνουμε δύο ομώνυμα κλάσματα;
ii. Πως συγκρίνουμε δύο ετερώνυμα κλάσματα;
«Απάντηση 7»
i. Όταν δύο κλάσματα είναι ομώνυμα, μεγαλύτερο είναι εκείνο που έχει μεγαλύτερο αριθμητή.
ii. Όταν έχουμε να συγκρίνουμε δύο ετερώνυμα κλάσματα τα μετατρέπουμε πρώτα σε ομώνυμα και κατόπιν να συγκρίνουμε σύμφωνα με τον προηγούμενο κανόνα.
Ερώτηση 8
Πως συγκρίνουμε ένα κλάσμα με τη μονάδα;
«Απάντηση 8»
Αν σε ένα κλάσμα
* ο αριθμητής είναι μικρότερος από τον παρονομαστή, τότε το κλάσμα είναι μικρότερο από το 1
* ο αριθμητής είναι ίσος με τον παρονομαστή, τότε το κλάσμα είναι ίσο με το 1
* ο αριθμητής είναι μεγαλύτερος από τον παρονομαστή, τότε το κλάσμα είναι μεγαλύτερο από το 1.
Ερώτηση 9
i. τι είναι η απλοποίηση κλάσματος;
ii. Πότε ένα κλάσμα λέγεται ανάγωγο;
«Απάντηση 9»
i. Όταν διαιρούμε τους όρους ενός κλάσματος με ένα κοινό διαιρέτη τους προκύπτει ένα νέο κλάσμα ίσο με το αρχικό αλλά με μικρότερους όρους. Η διαδικασία αυτή λέγεται απλοποίηση κλάσματος.
ii. Ανάγωγο λέγεται το κλάσμα που δεν απλοποιείται.
Ερώτηση 10
i. Πως προσθέτουμε ομώνυμα κλάσματα;
ii. Πως προσθέτουμε ετερώνυμα κλάσματα;
«Απάντηση 10»
i. Για να προσθέσουμε δύο ομώνυμα κλάσματα, κρατάμε τον ίδιο παρονομαστή και προσθέτουμε τους αριθμητές τους.
ii. Για να προσθέσουμε δύο ετερώνυμα κλάσματα τα μετατρέπουμε πρώτα σε ομώνυμα και μετά τα προσθέτουμε σύμφωνα με τον προηγούμενο κανόνα.
Ερώτηση 11
i. Πως αφαιρούμε ομώνυμα κλάσματα;
ii. Πως αφαιρούμε ετερώνυμα κλάσματα;
«Απάντηση 11»
i. Για να αφαιρέσουμε δύο ομώνυμα κλάσματα, κρατάμε τον ίδιο παρονομαστή και αφαιρούμε τους αριθμητές τους.
ii. Για να αφαιρέσουμε δύο ετερώνυμα κλάσματα τα μετατρέπουμε πρώτα σε ομώνυμα και μετά τα αφαιρούμε σύμφωνα με τον προηγούμενο κανόνα.
Ερώτηση 12
i. Πως πολλαπλασιάζουμε δύο κλάσματα;
ii. Πως διαιρούμε δύο κλάσματα;
«Απάντηση 12»
i. Για να πολλαπλασιάσουμε δύο κλάσματα πολλαπλασιάζουμε αριθμητή με αριθμητή και παρονομαστή με παρονομαστή.
ii. Για να διαιρέσουμε δύο κλάσματα πολλαπλασιάζουμε το πρώτο κλάσμα με το αντίστροφο του δεύτερου κλάσματος.
Ερώτηση 13
i. Ποιοι αριθμοί λέγονται αντίστροφοι; (δώστε και παράδειγμα)
ii. Όλοι οι αριθμοί έχουν αντίστροφο;
iii. Υπάρχει αριθμός που είναι ίσος με τον αντίστροφό του;
«Απάντηση 13»
i. Δύο αριθμοί που έχουν γινόμενο 1 λέγονται αντίστροφοι. Παράδειγμα οι αριθμοί 7/5 και 5/7.
ii. Ο αριθμός 0 δεν έχει αντίστροφο
(γιατί ότι πολλαπλασιάζετε με το μηδέν μηδενίζεται και επομένως δεν μπορεί το γινόμενο να είναι 1).
iii. Ο αριθμός 1 έχει αντίστροφο τον αριθμό 1.
(γιατί 1.1=1)
Ερώτηση 14
Τι ονομάζουμε κλίμακα ενός χάρτη;
«Απάντηση 14»
Ο λόγος της απόστασης δύο σημείων στο χάρτη προς την πραγματική απόσταση των δύο αντίστοιχων σημείων λέγεται κλίμακα του χάρτη. (εννοείται ότι οι αποστάσεις είναι μετρημένες με την ίδια μονάδα.)
Ερώτηση 15
Τι είναι η απόσταση δύο σημείων;
«Απάντηση 15»
Απόσταση δύο σημείων ονομάζουμε το μήκος του τμήματος που τα ενώνει.
Ερώτηση 16
Τι ονομάζουμε μέσο ευθύγραμμου τμήματος;
«Απάντηση 16»
Μέσο ευθύγραμμου τμήματος ονομάζουμε ένα σημείο, που ανήκει στο τμήμα και χωρίζει αυτό σε δύο ίσα τμήματα.
Ερώτηση 17
Τι είναι η διάμεσος τριγώνου;
«Απάντηση 17»
Το ευθύγραμμο τμήμα που ενώνει μια κορυφή ενός τριγώνου με το μέσο της απέναντι πλευράς, λέγεται διάμεσος του τριγώνου. Προφανώς κάθε τρίγωνο έχει τρεις διαμέσους που αν σχεδιαστούν σωστά παρατηρούμε ότι διέρχονται και οι τρεις από το ίδιο σημείο (λέγεται κέντρο βάρους του τριγώνου).
Ερώτηση 18
Τι ονομάζουμε ύψος τριγώνου;
«Απάντηση 18»
Η απόσταση της κορυφής ενός τριγώνου από την απέναντι πλευρά λέγεται ύψος του τριγώνου.
Ερώτηση 19
i. Ποιες είναι οι σχετικές θέσεις δύο ευθειών στο επίπεδο;
ii. Πότε δύο ευθείες του επιπέδου λέγονται παράλληλες;
«Απάντηση 19»
i. Δύο ευθείες που ανήκουν στο ίδιο επίπεδο μπορεί να είναι τεμνόμενες ή παράλληλες.
ii. Δύο ευθείες που ανήκουν στο ίδιο επίπεδο και δεν τέμνονται λέγονται παράλληλες.
Ερώτηση 20
i. Τι είναι κύκλος;
ii. Πότε λέμε ότι μια ευθεία εφάπτεται σε ένα κύκλο;
«Απάντηση 20»
i. Κύκλος με κέντρο Ο και ακτίνα ρ είναι το επίπεδο σχήμα που όλα του τα σημεία απέχουν από το Ο απόσταση ίση με ρ.
ii. Όταν μια ευθεία έχει ένα μόνο κοινό σημείο με ένα κύκλο τότε η ευθεία λέγεται εφαπτομένη του κύκλου. Το κοινό σημείο της ευθείας και του κύκλου λέγεται σημείο επαφής. Η ακτίνα στο σημείο επαφής και η εφαπτομένη σχηματίζουν ορθή γωνία.
Ερώτηση 21
i. Τι ονομάζουμε μεσοκάθετο ενός ευθύγραμμου τμήματος;
ii. Ποια είναι η χαρακτηριστική ιδιότητα της μεσοκαθέτου;
«Απάντηση 21»
i. Η ευθεία που διέρχεται από το μέσο ενός τμήματος και είναι κάθετη σ’ αυτό λέγεται μεσοκάθετος του τμήματος.
ii. Κάθε σημείο της μεσοκαθέτου ενός τμήματος ισαπέχει από τα άκρα του τμήματος.
Ερώτηση 22
i. Σε ποιες κατηγορίες χωρίζουμε τα τρίγωνα όταν το χαρακτηριστικό ως προς το οποίο τα εξετάζουμε είναι οι πλευρές τους;
ii. Σε ποιες κατηγορίες χωρίζουμε τα τρίγωνα όταν το χαρακτηριστικό ως προς το οποίο τα εξετάζουμε είναι οι γωνίες τους;

«Απάντηση 22»
i. Τα είδη των τριγώνων ως προς τις πλευρές τους είναι:
a. Ισόπλευρο, το τρίγωνο που έχει τρεις πλευρές ίσες.
b. Ισοσκελές, το τρίγωνο που έχει δύο πλευρές ίσες.
c. Σκαληνό, το τρίγωνο που όλες του οι πλευρές είναι άνισες.
ii. Τα είδη των τριγώνων ως προς τις γωνίες τους είναι:
a. Αμβλυγώνιο, το τρίγωνο που έχει μια γωνία αμβλεία.
b. Ορθογώνιο, το τρίγωνο που έχει μια γωνία ορθή.
c. Οξυγώνιο, το τρίγωνο που όλες του τις γωνίες οξείες.
Ερώτηση 23
Ποια τα είδη γωνιών;
«Απάντηση 23»
Τα είδη των γωνιών είναι:
i. Ορθή, η γωνία 90°
ii. Οξεία, η γωνία που είναι μικρότερη από 90°
iii. Αμβλεία, η γωνία που είναι μεγαλύτερη από 90°
Ακόμη χαρακτηριστικές περιπτώσεις γωνιών είναι και οι
iv. Μηδενική, η γωνία 0°
v. Ευθεία, η γωνία 180°
vi. Πλήρης, η γωνία 360°.
Ερώτηση 24
i. Ποιες γωνίες λέγονται παραπληρωματικές και ποιες κατακορυφήν;
ii. Ποια σχέση συνδέει δύο κατακορυφήν γωνίες;
iii. Πόσο είναι το άθροισμα των γωνιών κάθε τριγώνου;
«Απάντηση 24»
i. Δύο γωνίες που έχουν άθροισμα 180°, λέγονται παραπληρωματικές.
Κατακορυφήν λέγονται δύο γωνίες όταν έχουν την ίδια κορυφή και οι πλευρές της μιας γωνίας είναι προεκτάσεις των πλευρών της άλλης γωνίας.
ii. Δύο κατακορυφήν γωνίες είναι ίσες.
iii. Το άθροισμα των γωνιών κάθε τριγώνου είναι 180°.
Ερώτηση 25
i. Ποια είδη παραλληλογράμμων γνωρίζετε;
ii. Ποιες είναι οι ιδιότητες του παραλληλογράμμου;
«Απάντηση 25»
i. Τα είδη των παραλληλογράμμων είναι:
a. Πλάγιο παραλληλόγραμμο
b. Ορθογώνιο, το παραλληλόγραμμο που έχει όλες του τις γωνίες ίσες (=90°)
c. Ρόμβος, το παραλληλόγραμμο που έχει όλες τις πλευρές του ίσες.
d. Τετράγωνο, το παραλληλόγραμμο που έχει τις πλευρές του ίσες και τις γωνίες του ίσες (=90°).
ii. Σε κάθε παραλληλόγραμμο ισχύουν οι παρακάτω ιδιότητες:
a. Οι απέναντι πλευρές του είναι παράλληλες
b. Οι απέναντι πλευρές του είναι ίσες
c. Οι απέναντι γωνίες είναι ίσες
d. Οι διαγώνιες διχοτομούνται.
Ερώτηση 26
Πως υπολογίζουμε το εμβαδόν
i. Τριγώνου
ii. Παραλληλογράμμου
iii. Τραπεζίου;
«Απάντηση 26»
i. Το εμβαδόν ενός τριγώνου είναι ίσο με το μισό του γινομένου της βάσης του επί το ύψος.

$E=\frac{\beta\cdot\upsilon}{2}$

ii. Το εμβαδόν ενός παραλληλογράμμου είναι ίσο με το γινόμενο μιας βάσης του επί το αντίστοιχο ύψος.

$E=\beta\cdot\upsilon$

iii. Το εμβαδόν ενός τραπεζίου είναι ίσο με το ημιάθροισμα των βάσεών του επί το ύψος του.

$E=\frac{(B+b)\cdot\upsilon}{2}$

Προσδιορισμός του Συντελεστή Διεύθυνσης της Ευθείας

Δείτε με ποιους τρόπους μπορούμε να υπολογίσουμε το συντελεστή διεύθυνσης μιας ευθείας ανάλογα με τα δεδομένα της άσκησης. Το άρθρο απευθύνεται σε μαθητές της Β΄ Λυκείου και κυρίως σε αυτούς που παρακολουθούν την θετική ή την τεχνολογική κατεύθυνση.

Σε προηγούμενο άρθρο είδαμε πως μπορούμε να βρούμε την εξίσωση μιας ευθείας. Είχαμε αναφέρει λοιπόν ότι πρέπει να μας έχουν δοθεί οπωσδήποτε ο συντελεστής διεύθυνσης (λ) κι ένα σημείο Α(χ_Α,ψ_Α) της ευθείας. Μάλιστα είχαμε λύσει κι ένα παράδειγμα όπου και τα δύο (συντελεστής και σημείο) δίνονταν άμεσα. Σήμερα θα δούμε με ποιους τρόπους θα μπορούσαν να μας δώσουν (έμμεσα) το συντελεστή διεύθυνσης.

Μέσω της γωνίας που σχηματίζει η ευθεία με τον άξονα χ΄χ:
Αν η ευθεία (ε) η οποία ζητάμε σχηματίζει γωνία ω με τον άξονα χ΄χ, τότε ισχύει: λ_ε=εφω
Μέσω δύο σημείων Α και Β από τα οποία διέρχεται η ευθεία:
Έστω ότι η ευθεία (ε) που θέλουμε να βρούμε διέρχεται από τα σημεία Α(x_A,y_Α) και Β(x_Β,y_Β), τότε για το συντελεστή διεύθυνσης λ_ετης ευθείας (ε) ισχύει:
$\lambda_\epsilon=\frac{y_B-y_A}{x_B-x_A}$ (μόνο για το Λύκειο)
Μέσω της παραλληλίας της ζητούμενης ευθείας με μια άλλη ευθεία που μας έχουν δώσει:
Αν η ευθεία (ε) που ψάχνουμε είναι παράλληλη με μια ευθεία (δ) μας έχουν δώσει, τότε ισχύει: λ_ε = λ_δ.
Μέσω της καθετότητας της ζητούμενης ευθείας με άλλη ευθεία που μας έχει δοθεί:
Αν η ζητούμενη ευθεία (ε) είναι κάθετη σε δοσμένη ευθεία (δ), τότε ισχύει: $\lambda_\epsilon\cdot\lambda_\delta=-1$
Μέσω της παραλληλίας της ζητούμενης ευθείας με ένα διάνυσμα που μας έχουν δώσει (Β΄ Λυκείου Κατεύθυνση):
Αν η ευθεία που αναζητάμε είναι παράλληλη με ένα διάνυσμα που μας έχουν δώσει με συντελεστή λ_δ, τότε ισχύει: λ_ε = λ_δ.
Μέσω της καθετότητας της ζητούμενης ευθείας με ένα διάνυσμα που μας έχει δοθεί (Β΄ Λυκείου κατεύθυνση):
Αν η ευθεία μας είναι κάθετη σε κάποιο διάνυσμα που έχει συντελεστή διεύθυνσης λ_δ, τότε θα ισχύει: $\lambda_\epsilon\cdot\lambda_\delta=-1$ .

Συγκεντρώνοντας όλα τα παραπάνω σε ένα πίνακα έχουμε:

Eυθεία (ε) με…	Υπολογισμός του λ_ε
(ε) και χ΄χ να σχηματίζουν γωνία ω	λ_ε = εφω
(ε) να διέρχεται από Α(x_A,y_A) και Β(x_B,Y_B)	$\lambda_\epsilon=\frac{y_B-y_A}{x_B-x_A}$
(ε) παράλληλη προς την ευθεία (δ)	λ_ε = λ_δ
(ε) κάθετη με την ευθεία (δ)	$\lambda_\epsilon\cdot\lambda_\delta=-1$
(ε) παράλληλη με το διάνυσμα	λ_ε = λ_δ
(ε) κάθετη με το διάνυσμα	$\lambda_\epsilon\cdot\lambda_\delta=-1$

Και για να ολοκληρώσουμε αυτά που είχαμε πει για τον προσδιορισμό της εξίσωσης μιας ευθείας θα τελειώσουμε βλέποντας με ποιο άλλο τρόπο θα μπορούσαν να μας δώσουν ένα σημείο από το οποίο περνά η ευθεία. Αν λοιπόν δεν δοθεί άμεσα θα μπορούσε να δοθεί ως τομή δύο άλλων ευθειών. Στην περίπτωση αυτή για να βρούμε τις συντεταγμένες του σημείου που χρειαζόμαστε πρέπει να λύσουμε το σύστημα αυτών των δύο εξισώσεων (αυτό θα μπορούσε να γίνει μόνο για τις Γ΄ Γυμνασίου, Α΄ Λυκείου και στην Κατεύθυνση της Β΄ Λυκείου. Στη Β΄ Γυμνασίου το σημείο θα δίνεται άμεσα.

Επειδή το άρθρο είναι σχετικά μεγάλο τα απαραίτητα παραδείγματα θα τα λύσουμε στο επόμενο.

Συνεχίζεται…>>>

Η εξίσωση της Ευθείας

Η εξίσωση ψ=λχ+β είναι γνωστό ότι παριστάνει μια ευθεία. Όμως ποιος ο ρόλος του λ και ποιος του β στην εξίσωση αυτή;

Είναι γνωστό ότι η αλγεβρική μορφή της εξίσωσης μιας ευθείας είναι η

Γραφική παράσταση — Κάντε κλικ στην εικόνα να δείτε το ρόλο των λ και β

$y=\lambda\cdot\chi+\beta$ $(\epsilon)$ , όπου

ο (πραγματικός) αριθμός λ ονομάζεται «συντελεστής διεύθυνσης» και εκφράζει την κλίση της ευθείας σε σχέση με τονημιάξονα Οχ και
ο αριθμός β δηλώνει τη θέση πάνω στον άξονα ψ΄ψ από την οποία διέρχεται η ευθεία.

Αυτό με το οποίο θα ασχοληθούμε σήμερα είναι το πως μπορούμε να βρούμε την εξίσωση μιας ευθείας, δηλαδή με άλλα λόγια να υπολογίσουμε τους αριθμούς λ και β.

Για να μπορέσουμε να βρούμε την εξίσωση θα πρέπει οπωσδήποτε να γνωρίζουμε (να μας έχουν δώσει δηλαδή)

το συντελεστή διεύθυνσης (λ) και

ένα σημείο έστω Α(χ_Α,ψ_Α) από το οποίο διέρχεται η ευθεία που ψάχνουμε.

Για παράδειγμα ας βρούμε την ευθεία που έχει συντελεστή διεύθυνσης 2 και διέρχεται από το σημείο Α(1,3).

Λύση:

Η εξίσωση της ευθείας $(\epsilon)$ θα έχει τη μορφή:

$y=\lambda\cdot\chi+\beta$

όμως μας έχουν δώσει ότι το λ=2,

$y=2\cdot\chi+\beta$

Για να δούμε τώρα πως θα υπολογίσουμε το β.

Έχουμε αναφέρει σε προηγούμενο άρθρο ότι,

«Όταν η γραφική παράσταση μιας συνάρτησης διέρχεται από κάποιο σημείο, τότε οι συντεταγμένες του σημείου επαληθεύουν την εξίσωση (τον τύπο) της συνάρτησης αυτής»

κι έτσι

[warning]Όταν μας δίνουν εξίσωση ευθείας και σημείο από το οποίο διέρχεται η ευθεία αυτή πάντα αντικαθιστούμε τις συντεταγμένες του σημείου στην εξίσωση της ευθείας.[/warning]

Ας το εφαρμόσουμε στην συγκεκριμένη περίπτωση να δούμε. Αντικαθιστούμε λοιπόν το χ με τον αριθμό 1 και το ψ με τον αριθμό 3 κι έχουμε:

$y=2\cdot\chi+\beta$ ,για χ=1 και y=3

$3=2\cdot1+\beta$

προέκυψε λοιπόν μια εξίσωση με μοναδικό άγνωστο το β, το οποίο και υπολογίζουμε

$3-2=\beta\Leftrightarrow\beta=1$

Βρήκαμε λοιπόν ότι η ευθεία με συντελεστή διεύθυνσης λ=2 που διέρχεται από το σημείο Α(1,3) είναι η

y=2x+1.

Σχόλια:

Θυμηθείτε τι έχουμε αναφέρει προηγούμενα » όσα πράγματα μας ζητούν τόσα πρέπει και να μας δίνουν γιαυτό αναζητήστε τα στην εκφώνηση της άσκησης.

[notice]

Tip 1:

Πλήθος Ζητούμενων = Πλήθος Δεδομένων

[/notice]

Αυτή την άσκηση είμαι σίγουρος ότι θα την χαρακτηρίσετε ως εύκολη. Σας πληροφορώ όμως ότι είναι η μοναδική κατηγορία ασκήσεων στην αναζήτηση της εξίσωσης μιας ευθείας. Οποιαδήποτε άλλη κι αν δείτε δεν έχει τίποτα παραπάνω τίποτα λιγότερο. Αυτό που κάνει κάποιες ασκήσεις της κατηγορίας αυτής πιο σύνθετες είναι ο τρόπος με τον οποίο δίνονται τα απαραίτητα στοιχεία δηλαδή ο συντελεστής διεύθυνσης και το σημείο.
Ακριβώς στο επόμενο άρθρο μας θα δούμε αυτό ακριβώς το «παιχνίδι», με ποιους τρόπους είναι δυνατό να δοθεί (έμμεσα) το λ και με ποιους τρόπους το σημείο.

[important]

Tip 2:

Για να βρούμε την εξίσωση μιας ευθείας πρέπει απαραίτητα να μας δίνουν (άμεσα ή έμμεσα)

[gn_list style=»guard»]

το συντελεστή διεύθυνσης
ένα σημείο της.

[/gn_list]

[/important]

Μέχρι τότε μπορείτε εσείς να δοκιμάσετε να λύσετε την παρακάτω άσκηση και να μας στείλετε την απάντηση (στα σχόλια του άρθρου) καθώς κι οποιαδήποτε απορία έχετε, ή κάποιο σχόλιο που θέλετε να κάνετε.

Μπορείτε φυσικά να επικοινωνήσετε και με e-mail.

Άσκηση:

Να βρεθεί η ευθεία (3) που έχει συντελεστή διεύθυνσης διπλάσιο από τον συντελεστή διεύθυνσης της ευθείας (δ):2ψ+4χ=3 αν γνωρίζετε ότι το σημείο Α(-3,8) είναι σημείο της (ε).

Συνεχίζεται…>>>

Εξίσωση Ευθείας

Μια λυμένη άσκηση στην εξίσωση της ευθείας για τους μαθητές της Γ΄ Γυμνασίου που για τη λύση της επιλύουμε σύστημα.

Άσκηση:

Να βρεθεί η εξίσωση της ευθείας που διέρχεται από τα σημεία Α(2,7) και Β(1,-3).

Λύση:

Όπως ξέρουμε όλες οι ευθείες έχουν την ίδια αλγεβρική μορφή, όλες είναι της μορφή: $y=ax+b$ (εκτός από τις κατακόρυφες φυσικά)

Εμείς εδώ καλούμαστε να υπολογίσουμε τους αριθμούς $a$ και $b$ . Αφού λοιπόν μας ζητάνε δύο πράγματα θα πρέπει να μας έχουν δώσει και δύο πληροφορίες τις οποίες και θα πρέπει να εκμεταλλευτούμε.Προφανώς στη συγκεκριμένη άσκηση οι δύο πληροφορίες είναι ότι τα σημεία Α και Β είναι σημεία αυτής της ευθείας. Τι σημαίνει όμως αυτό για μας και πως μπορούμε να το χρησιμοποιήσουμε;

Δηλαδή, αν αντικαταστήσουμε τις συντεταγμένες του σημείου (x,y) στην εξίσωση της συνάρτησης, προκύπτει μια «αληθής» πρόταση. Αυτό λοιπόν θα κάνουμε κι εδώ, θα αντικαταστήσουμε τις συντεταγμένες των σημείων Α και Β στην εξίσωση $y=ax+b$ κι θα προκύψουν δύο εξισώσεις (με δύο άγνωστους, τους $a$ και $b$ .

Πράγματι,

για το σημείο Α(2,7) έχουμε

$7=2a+b$

ενώ για το σημείο Β(1,-3) έχουμε

$-3=a+b$

Στο σύστημα που προέκυψε αφαιρούμε τις δύο εξισώσεις κατά μέλη ώστε να «εξαφανιστεί» το $b$ και θα έχουμε την εξίσωση

$10=a$

Επανερχόμαστε τώρα σε μια από τις δύο εξισώσεις του συστήματος (προφανώς σε αυτή που θεωρούμε ευκολότερη), αντικαθιστούμε το $a$ με τον αριθμό 10 και υπολογίζουμε το $b$ .

Ας υποθέσουμε ότι επιλέγουμε την $-3=a+b$ που για $a=10$ δίνει

$-3=10+b$

$-10-3=b$

δηλαδή

$b=-13$

κι έτσι η ευθεία που ψάχναμε ήταν η:

$y=10x-13$

[gn_box type=»warning» title=»Tip 1″]

Όταν μας δίνουν εξίσωση ευθείας και σημείο από το οποίο διέρχεται η ευθεία αυτή πάντα αντικαθιστούμε τις συντεταγμένες του σημείου στην εξίσωση της ευθείας.[/gn_box]

[gn_box type=»warning» title=»Tip 2″]

Για να λύσουμε σύστημα που προέκυψε από εξίσωση ευθείας όπως στην παραπάνω άσκηση, ο συντομότερος τρόπος είναι να αφαιρέσουμε τις εξισώσεις κατά μέλη.[/gn_box]

Δοκιμάστε κι εσείς να λύσετε την παρακάτω άσκηση και στείλτε μας την απάντηση(στα σχόλια αυτού του άρθρου ή με email).

Να βρεθεί η εξίσωση της ευθείας που τέμνει τον άξονα χ΄χ στο σημείο με τετμημένη -1 ενώ τον ψ΄ψ στο σημείο με τεταγμένη 1. Καλή επιτυχία.

Συντάκτης pdouligerisΔημοσιεύτηκε την 17 Απριλίου 2010Κατηγορίες Άλγεβρα Γ΄Ετικέτες Άλγεβρα,Ευθεία15 σχόλια στο Εξίσωση Ευθείας

Πλοήγηση άρθρων

Προηγούμενη σελίδα Σελίδα 1 Σελίδα 2 Σελίδα 3