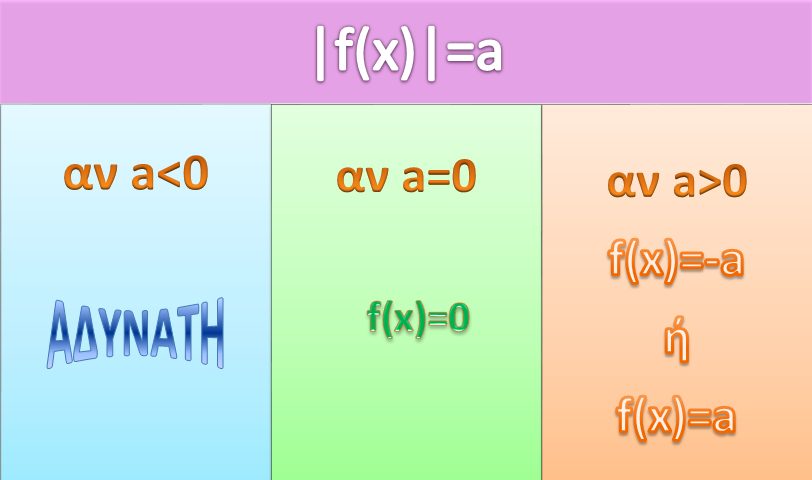Συντάκτης: pdouligeris
Κλάσμα
Το ![]() λέγεται κλάσμα και διαβάζεται «α προς β» ή και «α δια β».
λέγεται κλάσμα και διαβάζεται «α προς β» ή και «α δια β».
Ο αριθμός α είναι ο αριθμητής του κλάσματος ενώ ο αριθμός β λέγεται παρονομαστής.
Η γραμμή που χωρίζει τον αριθμητή από τον παρονομαστή λέγεται κλασματική γραμμή.
Σ΄ένα κλάσμα ο παρονομαστής δεν μπορεί να είναι 0.
Το κλάσμα α/β είναι το πηλίκο της διαίρεσης του α με το β. Δηλαδή ισχύει:
![]()
Βαθμός Πολυωνύμου
Βαθμό ενός πολυωνύμου μιας μεταβλητής ονομάζουμε τον αριθμό που είναι ίσος με τον μεγαλύτερο εκθέτη με τον οποίο εμφανίζεται η μεταβλητή του πολυωνύμου.
π.χ. το πολυώνυμο ![]() είναι 6ου βαθμού αφού το 6 είναι ο μεγαλύτερος εκθέτης στον οποίο εμφανίζεται το x. Ενώ το πολυώνυμο
είναι 6ου βαθμού αφού το 6 είναι ο μεγαλύτερος εκθέτης στον οποίο εμφανίζεται το x. Ενώ το πολυώνυμο ![]() είναι πρώτου βαθμού γιατί θυμίζουμε ότι t=t1.
είναι πρώτου βαθμού γιατί θυμίζουμε ότι t=t1.
Κάθε ακέραιος μη μηδενικός αριθμός μπορεί να θεωρηθεί ως πολυώνυμο (σε αυτή τη περίπτωση μιλάμε για σταθερό πολυώνυμο) μηδενικού βαθμού και αυτό γιατί για παράδειγμα ο αριθμός 4 θα μπορούσε να γραφτεί και ως 4=4.1=4.x0.
Ο αριθμός 0, που είναι κι αυτός πολυώνυμο, το λεγόμενο και μηδενικό πολυώνυμο, δεν έχει βαθμό.
Βαθμό ενός πολυωνύμου πολλών μεταβλητών ονομάζουμε το μεγαλύτερο από το άθροισμα των εκθετών κάθε όρου του.
Οι καλοί βαθμοί κάνουν καλό και στην … υγεία
 Οι καλοί βαθμοί των μαθητών δεν κάνουν καλό μόνο στην αυτοπεποίθησή τους, αλλά και στην υγεία τους ως ενηλίκων, σύμφωνα με μια νέα αμερικανική επιστημονική έρευνα. Προηγούμενες μελέτες έχουν δείξει ότι η εκπαίδευση συνδέεται με καλύτερη υγεία γενικά, αλλά η νέα έρευνα δείχνει συγκεκριμένα ότι οι καλύτερες επιδόσεις στο γυμνάσιο και το λύκειο παίζουν κρίσιμο ρόλο για την ύπαρξη καλύτερης υγείας σε όλη τη ζωή του ενήλικου.
Οι καλοί βαθμοί των μαθητών δεν κάνουν καλό μόνο στην αυτοπεποίθησή τους, αλλά και στην υγεία τους ως ενηλίκων, σύμφωνα με μια νέα αμερικανική επιστημονική έρευνα. Προηγούμενες μελέτες έχουν δείξει ότι η εκπαίδευση συνδέεται με καλύτερη υγεία γενικά, αλλά η νέα έρευνα δείχνει συγκεκριμένα ότι οι καλύτερες επιδόσεις στο γυμνάσιο και το λύκειο παίζουν κρίσιμο ρόλο για την ύπαρξη καλύτερης υγείας σε όλη τη ζωή του ενήλικου.
Οι ερευνητές που δημοσίευσαν τη σχετική μελέτη μελέτησαν περισσότερους από 10.000 μαθητές, που αποφοίτησαν από το σχολείο το 1957, και κατέγραψαν την πορεία της υγείας τους κατά τα επόμενα 53 χρόνια, μέχρι δηλαδή το 2010. Η έρευνα έδειξε ότι όσο καλύτεροι ήταν οι βαθμοί με τους οποίους αποφοίτησε ένας μαθητής, τόσο μικρότερη ήταν η πιθανότητα να επιδεινωθεί η υγεία του μελλοντικά, κοντά στην ηλικία συνταξιοδότησής του.
Μια πιθανή εκτίμηση (που όμως δεν προκύπτει από τα δεδομένα), σύμφωνα με τους ερευνητές, θα μπορούσε να είναι ότι το αίσθημα ευσυνειδησίας, που χαρακτηρίζει τους καλούς μαθητές, έχει ευεργετική επίδραση και στην κατοπινή υγεία τους, γιατί ως ενήλικοι αποφεύγουν με μεγαλύτερη ευκολία τις ανθυγιεινές συνήθειες στη ζωή τους.
Πόσο καλά τα πάει κανείς στο σχολείο, μετράει, όχι μόνο σε πράγματα όπως η εργασία και τα εισοδήματα, αλλά και στην υγεία, όπως αποδεικνύεται πλέον. Η ευεργετική επίδραση στην υγεία μπορεί να γίνει φανερή χρόνια ή και δεκαετίες μετά την αποφοίτηση από το σχολείο.
Όριο Συνάρτησης που δεν έχω τον τύπο της (1/2)
Πως βρίσκουμε το όριο μιας συνάρτησης f όταν δεν μας έχουν δώσει τον τύπο της αλλά μόνο ένα άλλο όριο στο οποίο όμως συμμετέχει και η f.
Γενικής Παιδείας Γ΄ Λυκείου

Υπάρχουν ασκήσεις στις οποίες ζητείται το όριο μιας συνάρτησης f της οποίας όμως δεν μας έχουν δώσει τον τύπο κι έτσι φαίνεται δύσκολο το να υπολογιστεί το όριο αυτό. Προφανώς όμως κάτι θα μας έχουν δώσει για την συνάρτηση αυτή και συνήθως μας δίνουν είτε ένα όριο στο οποίο συμμετέχει και η συνάρτηση f είτε μια διπλή ανισότητα στο κέντρο της οποίας υπάρχει η f. Αυτές τις δύο περιπτώσεις θα μελετήσουμε εδώ αλλά θα χωρίσουμε το άρθρο στα δύο για δύο κυρίως λόγους πρώτα γιατί προβλέπεται να είναι μεγάλο και θα σας κουράσει και δεύτερον γιατί η πρώτη περίπτωση (δεν δίνεται η f αλλά ένα όριο στο οποίο συμμετέχει η f ) αφορά και τους μαθητές της γενικής παιδείας ενώ η δεύτερη περίπτωση (δεν δίνεται η f αλλά δίνεται διπλή ανισότητα που στο κέντρο της εμφανίζεται η f ) αφορά μόνο μαθητές θετικής και τεχνολογικής κατεύθυνσης.
Ας ξεκινήσουμε λοιπόν με ένα παράδειγμα όπου
μας ζητούν το ![]()
καθώς και το ![]()
ενώ μας δίνουν ότι ισχύει: ![]()
Βλέπουμε λοιπόν εδώ ότι δεν γνωρίζουμε ποια είναι η συνάρτηση f το μόνο που ξέρουμε είναι ένα όριο στο οποίο όμως συμμετέχει και η συνάρτηση f. Θα προσπαθήσουμε λοιπόν να φτιάξουμε έναν «ψεύτικο» τύπο για τη συνάρτηση που μας ενδιαφέρει.
Αυτό το πετυχαίνουμε θεωρώντας σαν συνάρτηση όλο το «περιεχόμενο» του ορίου που μας έχουν δώσει. Δηλαδή, το ![]() το θεωρούμε σαν μια συνάρτηση την οποία και ονομάζουμε g.
το θεωρούμε σαν μια συνάρτηση την οποία και ονομάζουμε g.
Έχουμε τώρα γνωστά δύο πράγματα,
ένα ότι ![]() και
και
δεύτερον ότι το ![]()
Την πρώτη σχέση την λύνουμε ως προς f(x) και έτσι προκύπτει ο «ψεύτικος τύπος» για την f:
![]() απ’ όπου θα υπολογίσουμε το όριο της f με τη βοήθεια προφανώς και του γνωστού ορίου της g.
απ’ όπου θα υπολογίσουμε το όριο της f με τη βοήθεια προφανώς και του γνωστού ορίου της g.
Πράγματι,
![]()
![]()
Ας υπολογίσουμε τώρα και το άλλο όριο,
![]() παρατηρούμε ότι είναι της μορφής 0/0 (μην ξεχνάμε ότι το όριο της f το βρήκαμε 2). Πρέπει λοιπόν να κάνουμε άρση της απροσδιοριστίας «εμφανίζοντας και εξαφανίζοντας» τον παράγοντα x-3 που ευθύνεται για το 0/0 (καλό είναι να θυμηθείς πως γίνεται αυτό κάνοντας μια γρήγορη ανάγνωση εδώ), έτσι
παρατηρούμε ότι είναι της μορφής 0/0 (μην ξεχνάμε ότι το όριο της f το βρήκαμε 2). Πρέπει λοιπόν να κάνουμε άρση της απροσδιοριστίας «εμφανίζοντας και εξαφανίζοντας» τον παράγοντα x-3 που ευθύνεται για το 0/0 (καλό είναι να θυμηθείς πως γίνεται αυτό κάνοντας μια γρήγορη ανάγνωση εδώ), έτσι
![]()
![]()
![]()
![]()
![]()
![]()
Οι μαθητές της θετικής και τεχνολογικής κατεύθυνσης θα πρέπει να διαβάσουν και το 2ο μέρος κάνοντας κλικ εδώ >>>
Back 2 School but i’m stay cool

Επιτέλους έφτασε η ώρα να ζωντανέψουν ξανά τα σχολεία μας. Αν και όλα δείχνουν ότι φέτος θα έχουμε μια δύσκολη χρονιά ας κάνει ο καθένας από μας ότι περνάει από το χέρι του ώστε το κάθε σχολείο να μπορέσει να προσφέρει όσο το δυνατό περισσότερα στους μαθητές του και στη κοινωνία μας γενικότερα. Κι όταν λέω ο καθένας από εμάς προφανώς εννοώ καθηγητές, μαθητές και γονείς γιατί απ΄ότι φαίνεται από κανέναν άλλο δεν πρέπει να περιένουμε τίποτα. Καλή Σχολική Χρονιά λοιπόν εύχομαι σε όλους. Και για να έχουμε μια καλή αρχή νομίζω ότι θα χρειαστούμε τολάχιστον τα βιβλία μας για να δουλέψουμε.
Κατεβάστε λοιπόν από εδώ (σε μορφή zip, άρα θέλουν αποσυμπίεση):
- τα Σχολικά Βιβλία της Α΄ Γυμνασίου
- τα Σχολικά Βιβλία της Β΄ Γυμνασίου
- τα Σχολικά Βιβλία της Γ΄ Γυμνασίου
- τα Σχολικά Βιβλία της Α΄ Λυκείου
- τα Σχολικά Βιβλία της Β΄ Λυκείου
- τα Σχολικά Βιβλία της Γ΄ Λυκείου
Όσοι είναι μέλη του ιστότοπου αυτού μπορούν να βρουν στο forum και βοηθήματα για όλα τα μαθήματα Γυμνασίου και Λυκείου με θεωρία-λυμένα παραδείγματα-λυμένες τις ασκήσεις των σχολικών βιβλίων κ.α.(επειδή το υλικό είναι πολύ κι ο χρόνος που έχω είναι λίγος τα αρχεία θα ανεβαίνουν στο forum σταδιακά, γι’ αυτό μείνετε συντονισμένοι).
Όσοι δεν είστε μέλη μπορείτε να εγγραφείτε κάνοντας κλικ εδώ συμπληρώνοντας το email σας, ένα όνομα χρήστη της αρεσκείας σας. Θα σας σταλεί στο mail σας ένας κωδικός που θα χρησιμοποιήσετε για να συνδεθείτε. Με την πρώτη σας είσοδο μπορείτε να τον αλλάξετε με έναν κωδικό που έσεις επιθυμείτε.
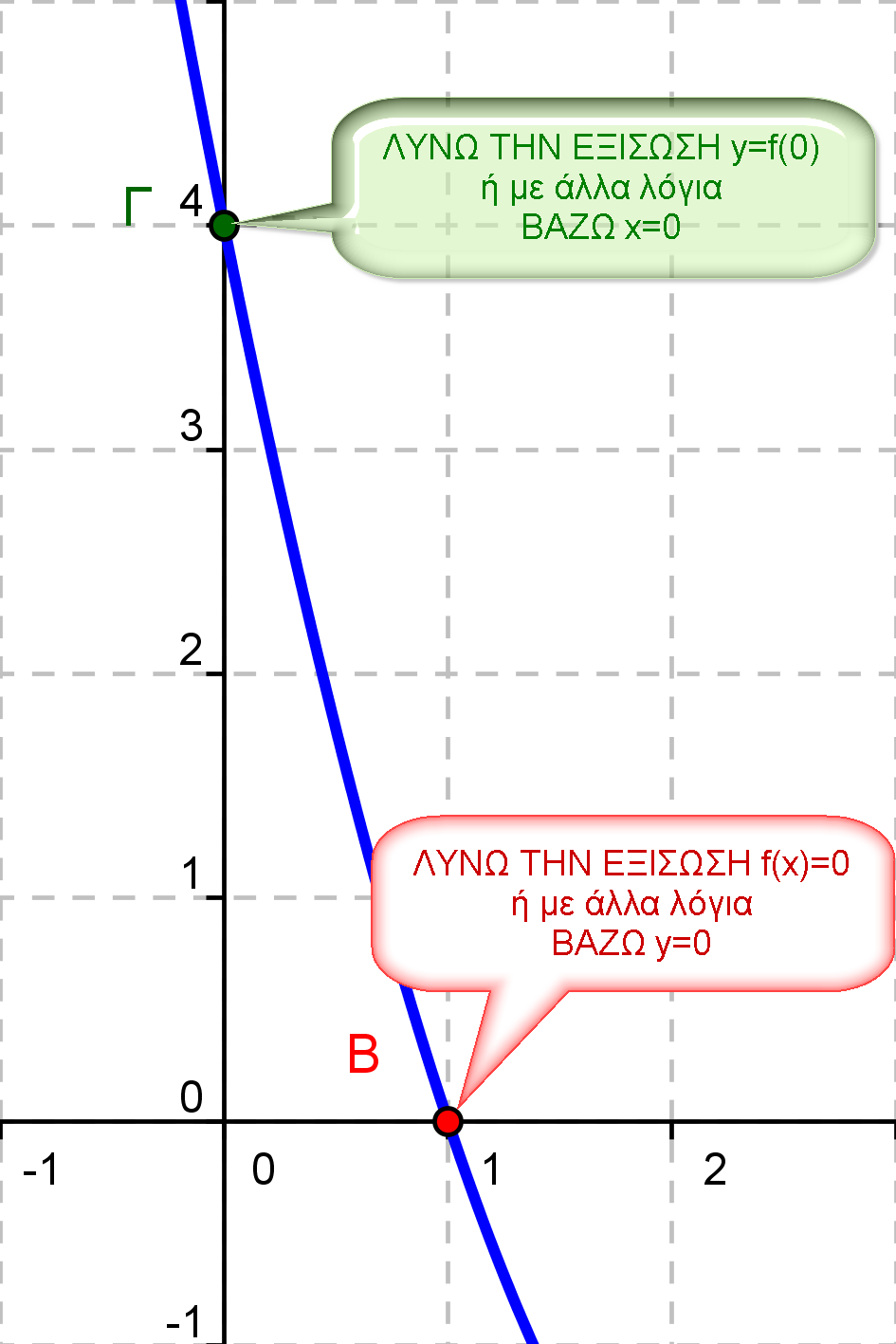
Θέλω να μάθω…πως βρίσκουμε τα σημεία που η γραφική παράσταση μιας συνάρτησης τέμνει τους άξονες
Ξέρουμε τον τύπο της συνάρτησης f και θέλουμε να βρούμε τα κοινά σημεία της γραφικής παράστασης της f με τους άξονες x’x και y’y.
ΑΛΓΕΒΡΑ Α΄ ΛΥΚΕΙΟΥ
 Όταν μας δίνεται ο τύπος μιας συνάρτησης στην ουσία μας δίνεται μια σχέση (ισότητα) που μας δείχνει τον τρόπο που συνδέονται μεταξύ τους τα x (=πρότυπα) με τα y (ή αλλιώς f(x)-εικόνες). Έτσι έχουμε τη δυνατότητα όταν γνωρίζουμε το x να μπορούμε να υπολογίσουμε την εικόνα του αλλά και το αντίστροφο όταν μας δίνουν το y μπορούμε εμείς να βρούμε το x. Ας πάρουμε για παράδειγμα τη συνάρτηση f με τύπο f(x)=4-x2. Για να βρω την εικόνα του 1 δεν έχω παρά να βάλω όπου x τον αριθμό 1 και να υπολογίσω το y. Έτσι θα έχω f(1)=4-12=3, δηλαδή η εικόνα του 1 είναι ο αριθμός 3. Αυτό μου δίνει και μια επιπλέον πληροφορία ότι η γραφική παράσταση της συνάρτησης f διέρχεται από το σημείο με συντεταγμένες (1,3). Αν τώρα μας ρωτήσουν ποιος αριθμός έχει εικόνα το -12 θα πρέπει εμείς να πάμε και πάλι στον τύπο της συνάρτησης και να βάλουμε όπου y (ή f(x) – το ίδιο είναι) τον αριθμό -12 και από τη σχέση αυτή να υπολογίσουμε το x. Ας το δούμε,
Όταν μας δίνεται ο τύπος μιας συνάρτησης στην ουσία μας δίνεται μια σχέση (ισότητα) που μας δείχνει τον τρόπο που συνδέονται μεταξύ τους τα x (=πρότυπα) με τα y (ή αλλιώς f(x)-εικόνες). Έτσι έχουμε τη δυνατότητα όταν γνωρίζουμε το x να μπορούμε να υπολογίσουμε την εικόνα του αλλά και το αντίστροφο όταν μας δίνουν το y μπορούμε εμείς να βρούμε το x. Ας πάρουμε για παράδειγμα τη συνάρτηση f με τύπο f(x)=4-x2. Για να βρω την εικόνα του 1 δεν έχω παρά να βάλω όπου x τον αριθμό 1 και να υπολογίσω το y. Έτσι θα έχω f(1)=4-12=3, δηλαδή η εικόνα του 1 είναι ο αριθμός 3. Αυτό μου δίνει και μια επιπλέον πληροφορία ότι η γραφική παράσταση της συνάρτησης f διέρχεται από το σημείο με συντεταγμένες (1,3). Αν τώρα μας ρωτήσουν ποιος αριθμός έχει εικόνα το -12 θα πρέπει εμείς να πάμε και πάλι στον τύπο της συνάρτησης και να βάλουμε όπου y (ή f(x) – το ίδιο είναι) τον αριθμό -12 και από τη σχέση αυτή να υπολογίσουμε το x. Ας το δούμε,
-12=4-x2 άρα 0=16-x2 δηλαδή (4-x)(4+x)=0 οπότε x=4 ή x= -4. Απαντάμε λοιπόν ότι οι αριθμοί -4 , 4 έχουν εικόνα τον -12. Πράγμα που σημαίνει ακόμη ότι η γραφική παράσταση της συνάρτησης f (συμβολίζεται με Cf ) περνάει από τα σημεία (-4,-12) και (4,-12). Τελειώσαμε με την εισαγωγή πάμε τώρα στο θέμα μας.
Θέλουμε να βρούμε τα σημεία που η γραφική παράσταση μιας συνάρτησης τέμνει τον άξονα x’x γνωρίζουμε όμως ότι όλα τα σημεία που βρίσκονται πάνω στον άξονα αυτό έχουν τεταγμένη μηδέν (y=0). Το ίδιο θα ισχύει και με το σημείο που ψάχνουμε άρα αρκεί να βάλουμε στον τύπο της συνάρτησης μας y=0 και να υπολογίσουμε το x. Ας χρησιμοποιήσουμε πάλι την ίδια συνάρτηση που χρησιμοποιήσαμε και πιο πάνω y=4-x2 η οποία για y=0 γίνεται 0=4-x2 δηλαδή 0=(2-x)(2+x) απ’ όπου προκύπτει x=-2 ή x=2. Επομένως γνωρίζουμε τώρα ότι η f τέμνει τον x’x στα σημεία με συντεταγμένες (-2,0) και (2,0)
Για να βρούμε το σημείο(αν υπάρχει θα είναι ένα και μοναδικό) που η γραφική παράσταση μιας συνάρτησης τέμνει τον άξονα y’y αρκεί να σκεφτούμε ότι όλα τα σημεία του άξονα αυτού έχουν τετμημένη ίση με μηδέν (x=0). Έτσι λοιπόν θα βάλουμε κι εμείς στον τύπο της συνάρτησης όπου x το αριθμό 0 και θα βρούμε πολύ εύκολα το y. Στην y=4-x2 για x=0 παίρνω y=4 και γνωρίζω πλέον ότι η f τέμνει τον y’y στο σημείο με συντεταγμένες (0,4).
Μπορούμε τώρα να καταλήξουμε στο παρακάτω συμπέρασμα:
[su_box color=»#0997FC» title=»Τομές γραφικής παράστασης με τους άξονες»][su_list style=»idea»]
Για να βρω που τέμνει η γραφική παράσταση της f
- τον x’x, βάζω στον τύπο της f y=0
- τον y’y, βάζω στον τύπο της f x=0
[/su_list][/su_box]
Ας δούμε και μερικά παραδειγματάκια τα οποία σας προτείνω να λύσετε μόνοι σας και στη συνέχεια να κάνετε κλικ στη «Λύση» για να τσεκάρετε αυτό που βρήκατε.
Άσκηση 1:
Να βρείτε σε ποιο σημείο τέμνει η
![]()
τον άξονα y’y
[wpspoiler name=»Λύση»]
Η f αν τέμνει τον y’y θα τον τέμνει στο σημείο με συντεταγμένες (0,f(0)). Αρκεί λοιπόν να βρούμε το f(0). Βάζουμε x=0 και έχουμε
![]()
Επομένως το σημείο είναι το (0,1)
Παρατήρηση: Μια συνάρτηση δεν είναι υποχρεωτικό να τέμνει τον άξονα y’y αυτό μπορεί να συμβαίνει για παράδειγμα σε μια συνάρτηση που το 0 δεν θα ανήκει στο πεδίο ορισμού της και κατά συνέπεια δεν θα υπάρχει το f(0) π.χ. η g(x)=1/x. Αν στο πεδίο ορισμού της συνάρτησης υπάρχει το 0 τότε μπορώ να βρω την εικόνα του άρα και το σημείο που τέμνει αυτή τον y’y. Το σημείο αυτό όμως θα είναι μοναδικό γιατί δεν γίνεται να δώσω στο x την τιμή 0 και να πάρω περισσότερα από ένα αποτελέσματα άλλωστε το λέει ξεκάθαρα και ο ορισμός της συνάρτησης ότι «σε κάθε x από το πεδίο ορισμού αντιστοιχεί ένα και μόνο y». Έτσι λοιπόν η γραφική παράσταση μιας συνάρτησης μπορεί να τέμνει τον y’y το πολύ σε ένα σημείο.
[/wpspoiler]
Άσκηση 2:
Αν η συνάρτηση
![]()
τέμνει τον y’y σε σημείο με τεταγμένη 1 να βρείτε το k.
[wpspoiler name=»Λύση»]Το σημείο που η f τέμνει τον y’y έχει συντεταγμένες (0,f(0)). Η άσκηση μας δίνει τη πληροφορία ότι το σημείο αυτό είναι το (0,1) άρα είναι «υποχρεωτικό» να ισχύει
![]()
![]()
![]()
![]()
![]()
[/wpspoiler]
Άσκηση 3:
Να βρείτε τα σημεία τομής των γραφικών παραστάσεων των συναρτήσεων
![]()
και
![]()
με τους άξονες.
[wpspoiler name=»Λύση»]
- Για την f έχουμε
Πεδίο ορισμού:![Rendered by QuickLaTeX.com \[\mathbb{R}-\{1\}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-f152f477a3b665bd0d3e7832cebe4d02_l3.png)
γιατί το x δεν μπορεί να πάρει την τιμή 1 αφού μηδενίζει τον παρονομαστή (x-1=0
 x=1)
x=1)
Τομή με τον y’y: Βάζω x=0 και παίρνω![Rendered by QuickLaTeX.com \[f(0)=\frac{0^2+0+2}{0-1}=-2\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-c06015202e505263dd3aeb0e1982c9e7_l3.png)
άρα τέμνει τον y’y στο (0,-2)
Τομές με τον x’x: Βάζω y=0 και παίρνω![Rendered by QuickLaTeX.com \[\frac{x^2+x+2}{x-1}=0\Leftrightarrow x^2+x+2=0\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-373c6412f4244b878864cdad11011063_l3.png)
η εξίσωση αυτή είναι δεύτερου βαθμού με διακρίνουσα αρνητική (Δ=12-4.1.2=-7) επομένως δεν έχει λύσεις πράγμα που σημαίνει ότι η γραφική παράσταση της f δεν τέμνει τον x’x.
Παρατήρηση: Η εξίσωση f(x)=0 είναι μια εξίσωση με άγνωστο το x και το πόσες λύσεις θα έχει εξαρτάται από τη μορφή που θα έχει ο τύπος της συνάρτησης μπορεί να είναι αδύνατη όπως αυτή που είδαμε μόλις τώρα και η Cf να μην τέμνει τον x’x αλλά μπορεί να έχει μια, δύο, τρεις ή και άπειρες λύσεις οπότε να τέμνει τον x’x σε δύο, τρία ή και άπειρα σημεία. - Για την g έχουμε
Πεδίο ορισμού:![Rendered by QuickLaTeX.com \[\mathbb{R}-\{0\}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-cbb312dd6a4ee481b3ae90eb6211e053_l3.png)
γιατί το x είναι παρονομαστής και δεν μπορεί να μηδενίζεται
Τομή με τον y’y: Βάζω x=0 ???? Προφανώς η Cg δεν τέμνει τον άξονα των y αφού δεν υπάρχει το g(0)
Τομές με τον x’x: Βάζω y=0 και λύνω την εξίσωση![Rendered by QuickLaTeX.com \[g(x)=0\Leftrightarrow\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-1486c3f2962f2ca98e29f69cddc0517a_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\left\{\begin{matrix}4x-12=8\\ \eta \\4x-12=-8 \end{matrix}\Leftrightarrow \left\{\begin{matrix}4x=20\Leftrightarrow x=5\\ \eta \\4x=4\Leftrightarrow x=1\end{matrix}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-334cae74292529eb6254713ee7ee42a1_l3.png)
επομένως η γραφική παράσταση της g τέμνει τον άξονα x’x στα σημεία (1,0) , (5,0)
[/wpspoiler]
Άσκηση 4:
Αν γνωρίζουμε ότι η συνάρτηση
![]()
τέμνει τον y’y στο σημείο με τεταγμένη 6 και τον x’x στα σημεία με τετμημένες 2 και 3 να βρεθούν τα a,b και c.
[wpspoiler name=»Λύση»]
Επειδή η f τέμνει τον y’y στο (0,6) θα πρέπει να ισχύει
![]()
Τώρα η συνάρτηση μας παίρνει τη μορφή
![]()
γνωρίζουμε όμως ότι τέμνει και τον x’x στα (2,0) και (3,0) επομένως θα ισχύει
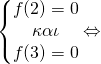
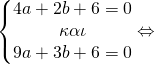
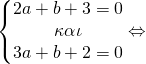
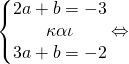
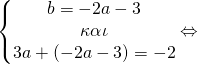
![]()
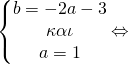
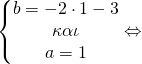
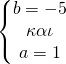
Έτσι μετά τη λύση του συστήματος βρήκαμε a=1, b=-5, c=6 οπότε και η f είναι η
![]()
[/wpspoiler]
Παραγοντοποίηση Τριωνύμου
Με ποιο τρόπο μετατρέπουμε σε γινόμενο ένα τριώνυμο; Τι ρόλο παίζουν οι ρίζες του τριωνύμου σε αυτή τη διαδικασία;
ΑΛΓΕΒΡΑ Γ΄ ΓΥΜΝΑΣΙΟΥ

![]()
συνήθως την ονομάζουμε τριώνυμο και νομίζω ότι είναι προφανής ο λόγος αφού όπως βλέπουμε αποτελείται από τρεις μόνο όρους. Τον δευτεροβάθμιο όρο «αx2«, τον πρωτοβάθμιο όρο «βx» και από τον σταθερό όρο «γ». Για το τριώνυμο έχουμε ξαναμιλήσει σε προηγούμενο άρθρο κι έχουμε ασχοληθεί με το πως μπορούμε να βρούμε τις ρίζες του, θυμίζουμε ότι ρίζες του τριωνύμου είναι οι λύσεις της εξίσωσης
![]()
(αν θέλετε να το διαβάσετε αναλυτικά κάντε κλικ εδώ αν θέλετε να θυμηθείτε στα γρήγορα τη διαδικασία κάντε κλικ εδώ να δείτε τη μεθοδολογία).
Τώρα θα ασχοληθούμε με το πως μπορούμε να παραγοντοποιήσουμε ένα τριώνυμο δηλαδή με ποιο τρόπο μπορούμε να μετατρέψουμε ένα τριώνυμο σε γινόμενο. Για την παραγοντοποίηση γενικά έχουμε αναφερθεί προηγούμενα εδώ. Επειδή όμως στο σχολικό βιβλίο η παραγοντοποίηση του τριωνύμου παρουσιάζεται αρκετά αργότερα, δεν το είχαμε αναφέρει καθόλου τότε. Έφτασε λοιπόν η ώρα να ασχοληθούμε και με αυτό το θέμα.
Όταν λοιπόν για κάποιο λόγο χρειαστεί ένα τριώνυμο να το κάνουμε γινόμενο δεν έχουμε παρά να βρούμε τις ρίζες του έστω x1 και x2 και στη συνέχεια να χρησιμοποιήσουμε τον τύπο:
[su_note color=»#0972FB»]
[/su_note]![]()
Ας δούμε ένα παράδειγμα: Έστω ότι θέλουμε να μετατρέψουμε σε γινόμενο το ![]() .
.
Πρώτα απ’ όλα πρέπει να βρούμε τις ρίζες του και για το λόγο αυτό λύνουμε την εξίσωση
![]()
.
Έχουμε 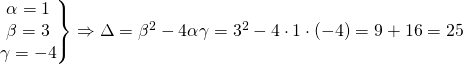
οπότε οι ρίζες είναι
![]()
![]()
Σύμφωνα με αυτά που αναφέραμε πιο πάνω παραγοντοποιούμε το τριώνυμο με τον τύπο και παίρνουμε
![]()
θα δούμε και δύο ακόμη παραδείγματα γιατί πιθανόν να δημιουργήθηκαν απορίες σε ορισμένους από εσάς για το τι κάνουμε στην περίπτωση που δεν έχουμε ρίζες ή στην περίπτωση που το τριώνυμο έχει διακρίνουσα ίση με μηδέν.
Αν ένα τριώνυμο όπως για παράδειγμα το x2+x+1 έχει διακρίνουσα αρνητική (Δ=-3) τότε όπως γνωρίζουμε δεν έχει ρίζες κι έτσι δεν μετατρέπεται σε γινόμενο.
Ενώ αν μας δωθεί για παραγοντοποίηση ένα τριώνυμο όπως το 4x2-12x+9 θα έχουμε
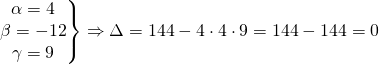
πράγμα που σημαίνει ότι έχουμε δύο ρίζες μόνο που στην περίπτωση αυτή θα είναι ίσες μεταξύ τους. Πράγματι
![]()
Έτσι χρησιμοποιώντας τον τύπο που δώσαμε παραπάνω παίρνουμε τελικά
![]()
το οποίο μάλλον θα ήταν πιο όμορφο αν το γράφαμε έτσι
![]()
![]()
![]()
![]()
![]()
Παρατηρούμε λοιπόν ότι ο τύπος για την παραγοντοποίηση τριωνύμου «δουλεύει» και όταν Δ>0 (δύο ρίζες διαφορετικές) αλλά και όταν Δ=0 (δύο ρίζες ίσες). Αν και όπως βλέπουμε κι από το προηγούμενο ακριβώς παράδειγμα το![]() μας δείχνει ότι το τριώνυμο ήταν ταυτότητα αλλά δεν το είχαμε προσέξει. Αυτό όμως είναι κανόνας που ισχύει πάντα «όταν η διακρίνουσα ενός τριωνύμου είναι ίση με μηδέν το τριώνυμο έχει δύο ρίζες ‘ισες χ1=χ2« κι επομένως θα ισχύει
μας δείχνει ότι το τριώνυμο ήταν ταυτότητα αλλά δεν το είχαμε προσέξει. Αυτό όμως είναι κανόνας που ισχύει πάντα «όταν η διακρίνουσα ενός τριωνύμου είναι ίση με μηδέν το τριώνυμο έχει δύο ρίζες ‘ισες χ1=χ2« κι επομένως θα ισχύει
![]()
Συνοψίζοντας λοιπόν όλα τα παραπάνω έχουμε:
[su_box title=»Μετατροπή τριωνύμου σε γινόμενο» color=»#0972FB»]
Το τριώνυμο ![]()
[su_list style=»arrow»]
- αν έχει Δ<0, δεν παραγοντοποιείται
- αν έχει Δ=0, γίνεται
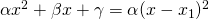
- αν έχει Δ>0, γίνεται
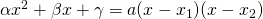
όπου ![]() οι ρίζες του. [/su_list][/su_box]
οι ρίζες του. [/su_list][/su_box]
Θέλω να μάθω … να λύνω εξισώσεις με απόλυτα
Για να λύσουμε εξισώσεις με απόλυτες τιμές (που ο άγνωστος είναι «φυλακισμένος» μέσα σε απόλυτα) πρέπει να ελευθερώσουμε τον άγνωστο από το απόλυτο. Πως μπορούμε να το πετύχουμε;
ΑΛΓΕΒΡΑ Α΄ ΛΥΚΕΙΟΥ
 Για το πως μπορούμε να απαλλαγούμε από τις απόλυτες τιμές που τυχόν εμφανίζονται σε μία αλγεβρική παράσταση έχουμε αναφερθεί σε προηγούμενο άρθρο μας (και καλό θα ήταν να του ρίξετε μια ματιά κάνοντας κλικ εδώ). Σε αυτή τη δημοσίευση θα ασχοληθούμε με εξισώσεις στις οποίες ο άγνωστος βρίσκεται πίσω από τις μπάρες της απόλυτης τιμής. Εξισώσεις δηλαδή που ο άγνωστος είναι «φυλακισμένος» μέσα σε μία ή και περισσότερες απόλυτες τιμές. Σκοπός μας σε μια τέτοια εξίσωση (όπως και σε κάθε εξίσωση άλλωστε) είναι να βρούμε ποιος αριθμός είναι «κρυμμένος πίσω από τη μάσκα του x». Στόχος μας είναι να «ελευθερώσουμε» το x μέσα από την απόλυτη τιμή. Για να το καταφέρουμε αυτό ας θυμηθούμε πρώτα τι είναι η απόλυτη τιμή ενός αριθμού και μετά βλέπουμε πως λύνουμε την εξίσωση.
Για το πως μπορούμε να απαλλαγούμε από τις απόλυτες τιμές που τυχόν εμφανίζονται σε μία αλγεβρική παράσταση έχουμε αναφερθεί σε προηγούμενο άρθρο μας (και καλό θα ήταν να του ρίξετε μια ματιά κάνοντας κλικ εδώ). Σε αυτή τη δημοσίευση θα ασχοληθούμε με εξισώσεις στις οποίες ο άγνωστος βρίσκεται πίσω από τις μπάρες της απόλυτης τιμής. Εξισώσεις δηλαδή που ο άγνωστος είναι «φυλακισμένος» μέσα σε μία ή και περισσότερες απόλυτες τιμές. Σκοπός μας σε μια τέτοια εξίσωση (όπως και σε κάθε εξίσωση άλλωστε) είναι να βρούμε ποιος αριθμός είναι «κρυμμένος πίσω από τη μάσκα του x». Στόχος μας είναι να «ελευθερώσουμε» το x μέσα από την απόλυτη τιμή. Για να το καταφέρουμε αυτό ας θυμηθούμε πρώτα τι είναι η απόλυτη τιμή ενός αριθμού και μετά βλέπουμε πως λύνουμε την εξίσωση.
Η απόλυτη τιμή ενός αριθμού ορίζεται και αλγεβρικά και γεωμετρικά. Εμείς θα αρκεστούμε στο δεύτερο μιας και είναι αρκετό για να στηριχτούμε σε αυτό και να καταφέρουμε να λύσουμε τις εξισώσεις.
Τι είναι λοιπόν η απόλυτη τιμή;
Γνωρίζουμε ότι κάθε πραγματικός αριθμός x παριστάνεται με ένα σημείο πάνω στον άξονα των πραγματικών αριθμών. Την απόσταση του σημείου αυτού από το 0 τη λέμε απόλυτη τιμή του αριθμού x και τη συμβολίζουμε |x|.

Έτσι μπορούμε να εξηγήσουμε και πολλές από τις ιδιότητες της απόλυτης τιμής όπως
Η απόλυτη τιμή οποιουδήποτε αριθμού είναι είτε θετικός αριθμός είτε μηδέν, γιατί όπως είναι γνωστό αρνητική απόσταση δεν υπάρχει. Έτσι έχουμε,
Οι αντίθετοι αριθμοί έχουν την ίδια απόλυτη τιμή, αφού ισαπέχουν από το 0.
Ας δούμε τώρα τι γίνεται με τις εξισώσεις.
Σας θυμίζω ότι για να αντιλαμβανόμαστε καλύτερα τις εξισώσεις μπορούμε να τις θεωρούμε σαν ερωτήσεις. Έτσι η εξίσωση |x|= -5 , μας ρωτάει ποιος αριθμός είναι αυτός που απέχει από το 0 -5 μονάδες; Προφανώς η απάντηση είναι κανένας (αναφέραμε και πιο πάνω ότι δεν νοείται αρνητική απόσταση). Ενώ η απάντηση στην ερώτηση(=εξίσωση) |x|=0 είναι «ο μοναδικός αριθμός που απέχει από το μηδέν 0 μονάδες είναι ο 0». Όμως η εξίσωση |χ|=2 μας ζητάει να βρούμε τον αριθμό που απέχει από το 0 2 μονάδες. Η απάντηση είναι ότι δεν υπάρχει μόνο ένας αριθμός με αυτή την ιδιότητα αλλά δύο αριθμοί ο 2 και ο -2. Έτσι η εξίσωσή μας έχει δύο λύσεις τις x=2 ή x= -2. Για να γενικεύσουμε λίγο τα πράγματα και να τα βάλουμε σε μία τάξη δείτε το παρακάτω σχεδιάγραμμα.

Όπου βλέπετε f(x) θα εννοούμε «μια παράσταση που περιέχει x». Γιατί μέσα στο απόλυτο δεν είναι απαραίτητο να υπάρχει μόνο x, μπορεί κάποιοι «κακοί μαθηματικοί» (σαν κι εμένα) να ζητήσουν να λυθούν εξισώσεις που μέσα στο απόλυτο να υπάρχουν αρκετά πράγματα.
Για να λύσουμε οποιαδήποτε εξίσωση στην οποία το x βρίσκεται μέσα σε απόλυτο, πρέπει να στηριχτούμε στα συμπεράσματα του παραπάνω πίνακα. Πρέπει λοιπόν να απομονώσουμε το απόλυτο στο ένα μέλος και μετά κοιτώντας τι ρόλο παίζει το άλλο μέλος να αποφανθούμε αν η εξίσωση έχει λύσεις ή όχι και στην περίπτωση που έχει ποιες είναι αυτές. Ας δούμε τώρα μερικά παραδείγματα:
Άσκηση 1: Να λυθεί η εξίσωση 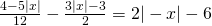
[gn_spoiler title=»Λύση:»]Φαίνεται η εξίσωση μας να έχει δύο διαφορετικές απόλυτες τιμές την |x| και την |-x|. Αυτό όμως δεν αληθεύει γιατί ξέρουμε ότι |-x|=|x|. Οπότε μπορούμε στην εξίσωση που μας δώσανε όπου έχει |-x| εμείς να βάλουμε |x|. Για να απομονώσουμε το απόλυτο που θέλουμε θα ακολουθήσουμε τη γνωστή διαδικασία που ακολουθούμε σε όλες τις εξισώσεις α΄ βαθμού.
Πρώτα θα διώξουμε τους παρονομαστές πολλαπλασιάζοντας κάθε όρο με το Ε.Κ.Π. των παρονομαστών που είναι το 12
![]()
![]()
Τώρα διώχνουμε τις παρενθέσεις κάνοντας χρήση της επιμεριστικής ιδιότητας
![]()
Χωρίζουμε τους γνωστούς από τους άγνωστους ώστε να μπορέσουμε να συνεχίσουμε τις πράξεις χωρίς να ξεχνάμε ότι προς το παρόν άγνωστος είναι το |x| κι όχι το x
![]()
![]()
άρα
![]()
ή πιο απλά
![]()
Αφού καταφέραμε κι απομονώσαμε το απόλυτο μπορούμε σύμφωνα με όσα έχουμε πει πιο πάνω ν΄απαντήσουμε ότι ![]() ή
ή ![]()
[/gn_spoiler]
Άσκηση 2: Να λυθεί η εξίσωση 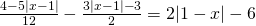
[gn_spoiler title=»Λύση:»]Όπως θα παρατηρήσατε η εξίσωση αυτή είναι ίδια με την προηγούμενη με την μόνη αλλαγή αντί για |x| έχουμε |x-1|. Και πάλι επειδή οι αριθμοί 1-x και x-1 είναι αντίθετοι η εξίσωση θα γίνει
![]()
και θα λυθεί με τον ίδιο ακριβώς τρόπο καταλήγοντας στο
![Rendered by QuickLaTeX.com \[|x-1|=2 \Leftrightarrow\left\{\begin{matrix}x-1=-2\Leftrightarrow x=-2+1=-1\\ \eta\\x-1=2\Leftrightarrow x=2+1=3\end{matrix}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-3d8b31a9400dddc58f39cee2363a52b1_l3.png)
Έτσι λοιπόν βλέπουμε ότι αν τα απόλυτα που έχουμε στην εξίσωση περιέχουν ίσες ή ακόμη και αντίθετες παραστάσεις, τότε δεν μας ενδιαφέρει το περιεχόμενη της απόλυτης τιμής. Λύνουμε την εξίσωση κανονικά όπως όλες τις εξισώσεις «κουβαλώντας» το απόλυτο μέχρι να καταφέρουμε να το απομονώσουμε και στο τέλος το πετάμε (πάντα σύμφωνα με το διάγραμμα που έχουμε παραπάνω).
Επειδή κάποιοι μπορεί να «ψιλό» μπερδεύονται κουβαλώντας το απόλυτο μπορούν να γλυτώσουν από αυτό με την συνηθισμένη στα μαθηματικά μέθοδο: «αν κάτι μ΄ενοχλεί κάνω πως δεν το βλέπω». Έτσι λοιπόν θα μπορούσαμε να θέσουμε όπου |x-1|=α (σχέση 1) και να λύσουμε την εξίσωση χωρίς το απόλυτο. Μόλις ξεμπερδέψουμε με το α και το βρούμε γυρίζουμε και το αντικαθιστούμε στη σχέση 1 απ’ όπου υπολογίζουμε το x που μας ενδιαφέρει.
Watch me 
Θέτω |χ-1|=α (σχέση 1) οπότε η εξίσωση γίνεται
![]()
![]()
![]()
![]()
![]()
Ας μην ξεχνάμε όμως ότι δεν ψάχναμε το α αλλά το x. Πάμε λοιπόν στη σχέση 1 και αντικαθιστούμε όπου α=2, οπότε
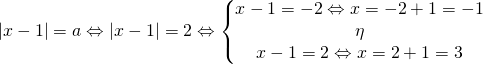
Τη μέθοδο αυτή για να είμαι ειλικρινής δεν σας την έδειξα μόνο για την περίπτωση που κάποιος δυσκολεύεται με τα πολλά απόλυτα αλλά και γιατί σε κάποιες περιπτώσεις θα έλεγα δεν μπορούμε να την αποφύγουμε γι’ αυτό καλό είναι να την ξέρουμε. Δείτε την επόμενη άσκηση και θα καταλάβετε. [/gn_spoiler]
Άσκηση 3: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση 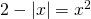
[gn_spoiler title=»Λύση:»] Την άσκηση αυτή θα μπορούσαμε να τη λύσουμε απομονώνοντας το απόλυτο στο ένα μέλος, οπότε η εξίσωση να γίνει |x|=2 – x2 αλλά πιστεύω ότι έτσι δεν θα μας συνέφερε γιατί το δεύτερο μέλος (το 2 – x2) δεν γνωρίζουμε αν είναι θετικός ή αρνητικός αριθμός ( για κάποιες τιμές του x γίνεται θετικός, για κάποιες αρνητικός και για κάποιες γίνεται ίσος με 0). Έτσι θα έπρεπε να διακρίνουμε περιπτώσεις και να πούμε
Περίπτωση 1η: αν το 2 – x2 είναι αρνητικό η εξίσωσή μας είναι αδύνατη (βλέπε και το σχεδιάγραμμα πιο πάνω)
Περίπτωση 2η: αν ![]() , τότε x=2-x2 ή x= – (2-x2 ) και να λύσω δύο εξισώσεις (δεύτερου βαθμού η καθεμία) κι αφού βρω τις λύσεις να κρατήσω από αυτές μόνο εκείνες που επαληθεύουν τον περιορισμό
, τότε x=2-x2 ή x= – (2-x2 ) και να λύσω δύο εξισώσεις (δεύτερου βαθμού η καθεμία) κι αφού βρω τις λύσεις να κρατήσω από αυτές μόνο εκείνες που επαληθεύουν τον περιορισμό ![]() .
.
Για να γλυτώσουμε όλη αυτή τη δουλειά μπορούμε να σκεφτούμε λίγο πιο έξυπνα και να αντικαταστήσουμε το |x| με έναν άλλο αριθμό έστω α. Τότε θα έχουμε γλυτώσει και από το |x| αλλά και από το x2 γιατί το x2=|x2|=|x|2=α2 (ρίξε μια ματιά στις ιδιότητες των απολύτων). Ας δούμε τώρα πως έχει καταντήσει η εξίσωσή μας θέτοντας |x|=α,
![]()
Η διακρίνουσα του τριωνύμου είναι
![]()
και οι λύσεις της εξίσωσης αυτής είναι
![]()
ή
![]()
Εύκολα λοιπόν βρήκαμε το α, το x όμως είναι αυτό που μας ενδιαφέρει
![Rendered by QuickLaTeX.com \[\left | x \right |=\alpha \Leftrightarrow \left\{\begin{matrix} \left | x \right |=1 \Leftrightarrow x=\pm 1\\\eta'\\ \left | x \right |=-2 & \alpha \delta \upsilon \nu \alpha \tau \eta \end{matrix}\right.\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-198fbd64d110d48053f6e400aa566f03_l3.png)
[/gn_spoiler]
Άσκηση 4: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση 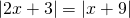
[gn_spoiler title=»Λύση:»] Στην άσκηση αυτή ανήκει στη γενική κατηγορία
![]()
και λύνεται με την ισοδυναμία
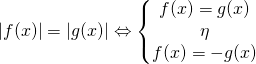
Έχουμε λοιπόν 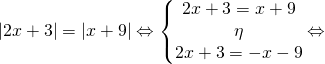
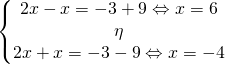 [/gn_spoiler]
[/gn_spoiler]
Σύνθεση Συναρτήσεων
Μαθηματικά Κατεύθυνσης Γ΄ Λυκείου. Πως βρίσκω αν ορίζεται η σύνθεση δύο συναρτήσεων και πως υπολογίζω τον τύπο της. Θα δείτε και λυμένα παραδείγματα «σύνθεσης» και «αποσύνθεσης» συναρτήσεων.
ΚΑΤΕΥΘΥΝΣΗ Γ΄ ΛΥΚΕΙΟΥ
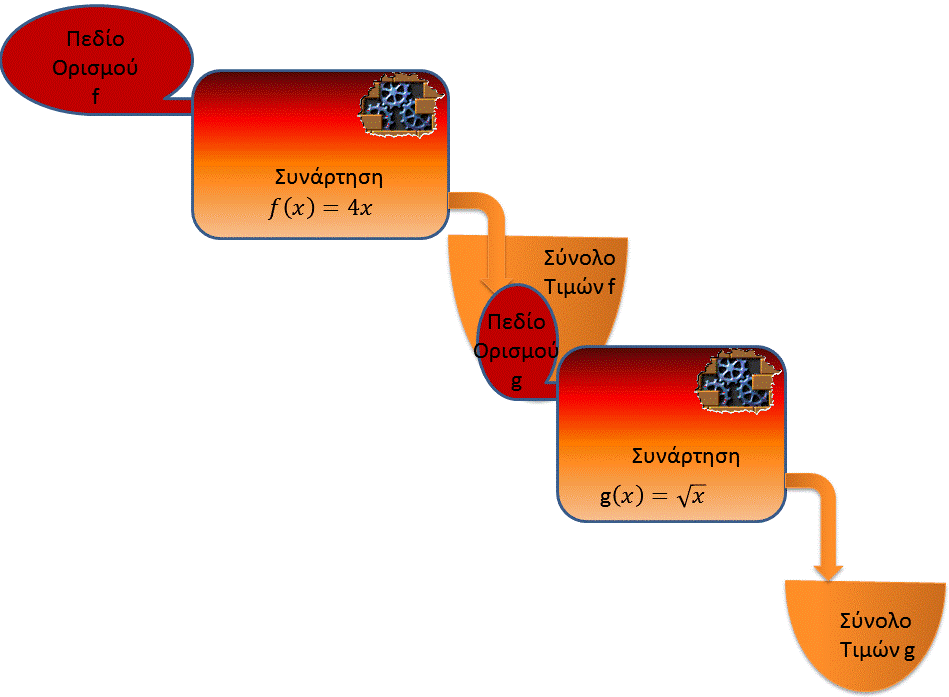
 Τη φετινή σχολική χρονιά με κάποιες τάξεις του σχολείου μας επισκεφτήκαμε ένα εργοστάσιο που εμφιάλωνε κρασί. Εκεί είδαμε ένα μηχάνημα που από τη μία μεριά έμπαιναν τα άδεια μπουκάλια κι από την άλλη έβγαιναν γεμάτα κρασί. Στη συνέχεια μια άλλη μηχανή έπαιρνε αυτά τα μπουκάλια και τα σφράγιζε. Στο τέλος μια ακόμη μηχανή κολλούσε σε αυτά ετικέτες ανάλογα με το περιεχόμενό τους. Κάπως έτσι μπορούμε να φανταστούμε και τις συναρτήσεις σαν μηχανές δηλαδή όπου από την μία μεριά δέχονται αντικείμενα και είναι προγραμματισμένες έτσι ώστε να μεταμορφώνουν αυτά τα αντικείμενα σε κάτι άλλο και να μας τα δίνουν πάλι μεταμορφωμένα. Κι όπως κάθε μηχάνημα έχει τις προδιαγραφές του για το τι αντικείμενα μπορεί να δεχτεί και το πρόγραμμά του που καθορίζει τι δουλεία μπορεί να κάνει, έτσι και οι συναρτήσεις έχουν τις προδιαγραφές τους για το τι αντικείμενα μπορούν να δεχτούν (οι συναρτήσεις που διδασκόμαστε στο σχολείο δέχονται μόνο αριθμούς, αλλά δεν υπάρχουν μόνο αυτές)- αυτό στα μαθηματικά το λέμε Πεδίο Ορισμού της συνάρτησης– κι έχουν κι ένα πρόγραμμα που μας δείχνει τι ακριβώς μπορεί να κάνει η συνάρτηση -αυτό είναι ο τύπος της.
Τη φετινή σχολική χρονιά με κάποιες τάξεις του σχολείου μας επισκεφτήκαμε ένα εργοστάσιο που εμφιάλωνε κρασί. Εκεί είδαμε ένα μηχάνημα που από τη μία μεριά έμπαιναν τα άδεια μπουκάλια κι από την άλλη έβγαιναν γεμάτα κρασί. Στη συνέχεια μια άλλη μηχανή έπαιρνε αυτά τα μπουκάλια και τα σφράγιζε. Στο τέλος μια ακόμη μηχανή κολλούσε σε αυτά ετικέτες ανάλογα με το περιεχόμενό τους. Κάπως έτσι μπορούμε να φανταστούμε και τις συναρτήσεις σαν μηχανές δηλαδή όπου από την μία μεριά δέχονται αντικείμενα και είναι προγραμματισμένες έτσι ώστε να μεταμορφώνουν αυτά τα αντικείμενα σε κάτι άλλο και να μας τα δίνουν πάλι μεταμορφωμένα. Κι όπως κάθε μηχάνημα έχει τις προδιαγραφές του για το τι αντικείμενα μπορεί να δεχτεί και το πρόγραμμά του που καθορίζει τι δουλεία μπορεί να κάνει, έτσι και οι συναρτήσεις έχουν τις προδιαγραφές τους για το τι αντικείμενα μπορούν να δεχτούν (οι συναρτήσεις που διδασκόμαστε στο σχολείο δέχονται μόνο αριθμούς, αλλά δεν υπάρχουν μόνο αυτές)- αυτό στα μαθηματικά το λέμε Πεδίο Ορισμού της συνάρτησης– κι έχουν κι ένα πρόγραμμα που μας δείχνει τι ακριβώς μπορεί να κάνει η συνάρτηση -αυτό είναι ο τύπος της.
Σχηματικά λοιπόν θα μπορούσαμε να παραστήσουμε τις συναρτήσεις έτσι όπως φαίνονται στις παρακάτω εικόνες 1 και 2.
Όπου βλέπουμε μια μηχανή (=συνάρτηση) με το όνομα f στην οποία μπαίνουν όλοι οι πραγματικοί αριθμοί (έχει πεδίο ορισμού όλο το R) και από την άλλη βγαίνουν 4 φορές μεγαλύτεροι αφού ο τύπος της f είναι f(x)=4x(εικόνα1)

Και στην εικόνα 2 παρακάτω βλέπουμε τη συνάρτηση g που δέχεται μόνο θετικούς αριθμούς (αφού έχει πεδίο ορισμού το R+) Continue reading «Σύνθεση Συναρτήσεων»