Συντάκτης: pdouligeris

Γραφική Παράσταση Ευθείας – Khan Academy

Μια σειρά ασκήσεων από Khan Academy στην ενότητα Εξίσωση Ευθείας
[khan_exercise src=’static:graphing_linear_equations’ /]

Λυμένες Ασκήσεις στην Εξίσωση της Ευθείας

4 λυμένες ασκήσεις στην εξίσωση της ευθείας.

Αφού έχουμε διαβάσει τα άρθρα:

  1. Η εξίσωση της ευθείας (θεωρία)
  2. Προσδιορισμός του συντελεστή διεύθυνσης μιας ευθείας (θεωρία – μεθοδολογία)

μπορούμε να δούμε μερικά παραδείγματα για να κατανοήσουμε καλύτερα το πως δουλεύουμε σε ασκήσεις που μας ζητάνε να

lines
Σύνθεση με ευθείες γραμμές :)

βρούμε την εξίσωση κάποιας ευθείας.

Να βρεθεί η εξίσωση της ευθείας (ε) στις παρακάτω περιπτώσεις:

1. Διέρχεται από το σημείο Α(2,1) και σχηματίζει με τον άξονα χ΄χ γωνία ω=45ο.

Λύση: Η εξίσωση που ζητάμε θα έχει τη μορφή: \psi=\lambda\chi+\beta.

Όμως λ=εφω=εφ45ο=1, κι έτσι η εξίσωση παίρνει τη μορφή \psi=\chi+\beta.

Κι επειδή το σημείο Α(2,1) είναι σημείο αυτής της ευθείας θα πρέπει να ισχύει: 1=2+\beta, δηλαδή β=-1.

Οπότε η ζητούμενη ευθεία είναι η \psi=\chi-1.

2. Διέρχεται από το σημείο Α(1,-1) και είναι παράλληλη στην ευθεία (δ): 2χ+ψ-1=0.

Λύση: Η ευθεία που ζητάμε είναι της μορφής \psi=\lambda\chi+\beta. Επειδή ε//δ θα ισχύει λε=λδ, αλλά ο συντελεστής διεύθυνσης της (δ) είναι λδ=-2, (γιατί (δ): 2χ+ψ-1=0 ή (δ): ψ=-2χ+1) κι έτσι λε=λδ=-2.

Η ευθείας μας λοιπόν έχει τώρα τη μορφή \psi=-2\chi+\beta. Περνάει όμως από το σημείο Α(1,-1) πράγμα που σημαίνει ότι θα ισχύει -1=-2(+1)+\beta\Leftrightarrow\beta=1. Τελικά η ευθεία (ε) είναι η \psi=-2\chi+3.

3. Διέρχεται από το Α(-1,1) και είναι κάθετη στην (δ):ψ=-2χ-1.

Λύση: λδ=-2, όμως (ε) κάθετη με τη (δ) άρα έχουμε \lambda_\epsilon\cdot\lambda_\delta=-1\Leftrightarrow\lambda_\epsilon=1/2. Η ευθεία που ψάχνουμε λοιπόν θα είναι κάπως έτσι: ψ=1/2χ+β.

Για να βρούμε το β τώρα μας αρκεί το γνωστό σημείο της ευθείας το Α(-1,1) γιατί ξέρουμε ότι θα ισχύει 1=\frac{1}{2}\cdot(-1)+\beta\Leftrightarrow\beta=\frac{3}{2} άρα η ευθεία μας είναι η ψ=1/2χ+3/2.

4. Τέμνει τους άξονες στα σημεία Α(4,0) και Β(0,4)

linesΛύση: Υπολογίζουμε το λ, \lambda=\frac{\psi_2-\psi_1}{\chi_2-\chi_1}=\frac{4-0}{0-4}=-1. Επομένως η εξίσωση της ευθείας θα έχει τη μορφή ψ=-χ+β. Όσον αφορά στο β τώρα θα χρησιμοποιήσουμε ένα από τα δύο σημεία από τα οποία διέρχεται η ευθεία που ζητάμε. Έστω λοιπόν ότι χρησιμοποιούμε το Β(0,4) και με αντικατάσταση παίρνουμε 4=-0+β ή β=4. Καταλήξαμε λοιπόν στο ότι η ζητούμενη ευθεία είναι η ψ=-χ+4.

Παρατηρήσεις:

Οι παρακάτω παρατηρήσεις αφορούν μαθητές της Β΄και Γ΄τάξης του Λυκείου που ακολουθούν τη θετική ή την τεχνολογική κατεύθυνση.

Παρατήρηση 1:

Οι παραπάνω ασκήσεις θα μπορούσαν προφανώς να λυθούν πιο εύκολα με τη χρήση του τύπου

    \[\psi-\psi_0=\lambda(\chi-\chi_0)\]

όπου Μ(χ0,ψ0) ένα σημείο της ευθείας και λ ο συντελεστής διεύθυνσής της. Να το δούμε σαν εφαρμογή στην παρακάτω άσκηση:

Να βρεθεί η μεσοκάθετη του τμήματος ΑΒ με Α(-2,1) και Β(2,3)

Λύση: Ο συντελεστής διεύθυνσης της ΑΒ είναι

    \[\lambda_{AB}=\frac{\psi_2-\psi_1}{\chi_2-\chi_1}=\frac{3-1}{2+2}=1/2\]

κι επειδή η μεσοκάθετη της ΑΒ είναι κάθετη με την ΑΒ θα ισχυεί:

    \[\lambda\cdot\lambda_{AB}=-1\Leftrightarrow\lambda=-2\]

.

Η μεσοκάθετη της ΑΒ θα διέρχεται από το μέσο του ΑΒ που είναι το Μ(\frac{\chi_2+\chi_1}{2} ,\frac{ \psi_2+\psi_1}{2})  δηλαδή Μ(\frac{2-2}{2} , \frac{3+1}{2})=(0,2).

Έτσι η μεσοκάθετη έχει την εξίσωση:

    \[\psi-\psi_0=\lambda(\chi-\chi_0)\Leftrightarrow\psi-0=-2(\chi-2)\Leftrightarrow\psi=-2x+4\]

, αφού έχει συντελεστή διεύθυνσης το λ=-2 και διέρχεται απο το Μ(0,2).

Παρατήρηση 2:

Σε όλα όσα έχουμε αναφέρει μέχρι τώρα γιά την εξίσωση της ευθείας έχουμε κάνει μια σημαντική παράλειψη. Είδαμε πως γιά να βρούμε την εξίσωση μιας ευθείας πρέπει οπωσδήποτε να μας δίνεται ένα σημείο της έστω Μ(α,β). Από ‘κει και πέρα υπολογίζω το λ (μέσω της γωνίας που σχηματίζει με τον χ΄χ ή μέσω μιας σχέσης παραλληλίας ή μιας σχέσης καθετότητας ή τέλος από δύο σημεία της ευθείας). Και τελικά βρίσκω την εξίσωση από τον τύπο ψ=λχ+μ ή από τον \psi-\psi_0=\lambda(\chi-\chi_0). Κι εδώ βρίσκεται το λάθος γιατί από το σημείο Μ(α,β) διέρχονται άπειρες ευθείες αλλά οι παραπάνω τύποι μας δίνουν μόνο την οριζόντια και τις πλάγιες που διέρχονται από το Μ κι όχι την κατακόρυφη κι αυτό γιατί για την κατακόρυφη δεν υπάρχει (δεν ορίζεται) συντελεστής διεύθυνσης. Αυτό σημαίνει ότι με τον τύπο \psi-\beta=\lambda(\chi-\alpha) έχω «χάσει» μια ευθεία που διέρχεται από το Μ(α,β) και συγκεκριμμένα την χ=α. Πρέπει λοιπόν όταν ξεκινάμε να λύσουμε μια άσκηση στην οποία ψάχνουμε μια ευθεία που διέρχεται από κάποιο σημείο π.χ. το Μ(1,3) να λέμε: «από το Μ(1,3) διέρχονται οι ευθείες χ=1 (κατακόρυφη) και οι ευθείες ψ-3=λ(χ-1)» στη συνέχεια να εξετάζουμε αν η κατακόρυφη ικανοποιεί τα δεδομένα του προβλήματος οπότε είναι αυτή που ψάχνουμε κι αν όχι συνεχίζουμε με τις υπόλοιπες. Ας δούμε ένα παράδειγμα και τέλος γιατί έχω την εντύπωση ότι αρκετά σας κούρασα.

Να βρεθεί η ευθεία που είναι κάθετη στο διάνυσμα \vec{a}=(3,0) και διέρχεται από το Μ(4,5).

Λύση: Από το Μ(4,5) διέρχονται οι ευθείες χ=4 (κατακόρυφη) και οι ευθείες ψ-5=λ(χ-4). Επειδή ο συντελεστής διεύθυνσης του διανύσματος είναι λ=ψ/χ=0/3=0, το διάνυσμα είναι οριζόντιο (παράλληλο στον χ΄χ) κι έτσι η ευθεία που ζητάμε θα είναι κατακόρυφη κι αφού πρέπει να περνάει από το Μ(4,5) είναι η χ=4.

Πράξεις με μιγαδικούς

Αφού γνωρίσαμε το σύνολο των μιγαδικών αριθμών ήρθε ο καιρός να δούμε και πως μπορούμε να κάνουμε πράξεις μέσα σε αυτό το σύνολο. Πριν ξεκινήσουμε όμως καλό θα ήταν να αναφερθούμε και στη ισότητα των μιγαδικών. Έστω λοιπόν ότι έχουμε δύο μιγαδικούς, τον z1=x1+y1i και τον z2=x2+y2i, τότε

Ισότητα μιγαδικών

Δύο μιγαδικοί z_1=x_1+y_1i , z_2=x_2+y_2i θα λέμε ότι είναι ίσοι αν έχουν ίσα πραγματικά αλλά και φανταστικά μέρη. Δηλαδή,z_1=z_2\Leftrightarrow\left\{\begin{matrix} x_1=x_2\\ \kappa \alpha \iota \\ y_1=y_2 \end{matrix}

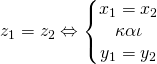
Από εδώ προκύπτει και το πότε ένας μιγαδικός θα είναι ίσος με 0. Πράγματι ένας μιγαδικός z=x+yi θα είναι ίσος με μηδέν (0=0+0i) αν και μόνο αν ισχύει x=0 και y=0.

Πρόσθεση κι αφαίρεση:

Πρόσθεση Μιγαδικών

Για να προσθέσουμε (ή να αφαιρέσουμε) μιγαδικούς προσθέτουμε (ή αφαιρούμε) τα πραγματικά τους μέρη και το ίδιο κάνουμε με

τα φανταστικά τους μέρη. Δηλαδή,z_1+z_2=(x_1+y_1i)+(x_2+y_2i)=(x_1+x_2)+(y_1+y_2)i z_1-z_2=(x_1+y_1i)-(x_2+y_2i)=(x_1-x_2)+(y_1-y_2)i

Παράδειγμα: (3+12i)+(5-4i)=(3+5)+(12-4)i=8+8i

Πολλαπλασιασμός μιγαδικών:

Γιά να πολλαπλασιάσουμε τους μιγαδικούς z1 και z2 κάνουμε χρήση της γνωστής μας επιμεριστικής ιδιότητας κι έτσι έχουμε,

    \[z_1\cdot z_2=(x_1+y_1i)(x_2+y_2i)=x_1x_2+x_1y_2i+y_1x_2i+y_1y_2i^2=\]

    \[(x_1x_2-y_1y_2)+(x_1y_2+x_2y_1)i\]

(θυμηθείτε ότι i2=-1)

Αν ο z1 είναι πραγματικός, δηλαδή z1=λ, τότε λz2=λ(x2+y2i)=λx2+λy2i.

Παράδειγμα: (1-2i)(3-4i)=3-4i-6i+8i2=3-8-4i-6i=-5-10i

Μέχρι εδώ όλα καλά κι εύκολα το μόνο που μας έμεινε ακόμη είναι να δούμε πως διαιρούμε μιγαδικούς αριθμούς. Πριν όμως αναφερθούμε στη διαίρεση θα χρειαστεί να ορίσουμε τον «συζυγή» ενός μιγαδικού. Κάτι αντίστοιχο είχαμε κάνει και για να ορίσουμε την πράξη της διαίρεσης στους ρητούς αριθμούς. Πρώτα είδαμε τι ονομάζεται αντίστροφος ενός αριθμού και μετά είπαμε ότι γιά να διαιρέσουμε δύο ρητούς πολλαπλασιάζουμε τον διαιρετέο με τον αντίστροφο του διαιρέτη. Κάτι ανάλογο κάνουμε κι εδώ.

Συζυγής ενός μιγαδικού:Συζυγείς Μιγαδικοί

Αν θεωρήσουμε το μιγαδικό z=x+yi, ονομάζουμε συζυγή του z και τον συμβολίζουμε με \bar{z} τον μιγαδικό x-yi. Δηλαδή 

    \[z=x+yi\Leftrightarrow\bar{z}=x-yi\]

Προφανώς ισχύουν και τα παρακάτω:

Ο z είναι πραγματικός αν και μόνο αν 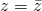z=\bar{z} και ο z είναι φανταστικός αν και μόνο αν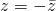 z=-\bar{z}

Την απόδειξη των παραπάνω καθώς και άλλες σχέσεις που αφορούν στο συζυγή ενός μιγαδικού θα δούμε σε επόμενο άρθρο για να μη βγούμε τώρα εκτός θέματος. Αυτό που θα χρειαστούμε όμως για τη διαίρεση, που σκοπεύουμε να καταλήξουμε, είναι η σχέση:

αν z=x+yi, τότε ισχύει:

    \[z \bar{z}=x^2+y^2\]

Πράγματι,

    \[z \bar{z}=(x+yi)(x-yi)=x^2-y^2i^2=x^2+y^2\]

Τώρα νομίζω είμαστε έτοιμοι να ορίσουμε και τη διαίρεση

Διαίρεση μιγαδικών:

Γιά να βρούμε το πηλίκο  δύο μιγαδικών z1 και z2, πολλαπλασιάζουμε και διαιρούμε με τον συζυγή του παρονομαστή. Δηλαδή,

    \[\frac{z_1}{z_2}=\frac{z_1 \bar{z_2}}{z_2 \bar{z_2}}=\frac{z_1 \bar{z_2}}{x_2^2+y_2^2}\]

Παράδειγμα: \frac{1-2i}{3+4i}=\frac{(1-2i)(3-4i)}{(3+4i)(3-4i)}=\frac{3-4i-6i+8i^2}{3^2+4^2}= \frac{-5-10i}{25}=-\frac{5}{25}-\frac{10}{25}i=-\frac{1}5-\frac{2}5i